数据结构与算法
数据的物理结构
数据存储在存储器当中,而存储器相当于内存而言,而光盘,软盘,硬盘等外部存储器的数据组织通常用文件结构来描述。数据存储的形式有两种:顺序式和链式。、
算法的五个特征:输入,输出,有穷性,确定性和可行性。
特征 解释 输入 0个或者多个 输出 一个或者多个输出 有穷性 不会无限循环 确定性 确定性不会有其他含义 可行性 每一步都是可行的 算法的设计要求
1、没有语法错误。
2、算法程序对于合法输入能够产生满足要求的输出。
3、算法程序对于非法输入能产生满足规格的说明。
4、算法对于故意刁难的测试输入都有满足要求的输出结果。
可读性
需要便于后续的修改阅读
健壮性
输入不合理时,算法能够有相应的处理,而不是产生异常、崩溃或者莫名奇妙的结果。
时间效率高和存储量
1、时间复杂度
关键在于认识: 时间=执行次数
T(n)=O(f(n));
这样就可以用O来记时间复杂度
一般情况下,随着输入规模n的增大,T(n)增长最慢的算法为最优算法。
常见的时间复杂度O(1),O(n),O(n^2),O(log(n)),O(nlog(n)),O(n^3),O(2^n),O(n!),O(n^n)
2、空间复杂度
关键在于认识: 空间=占用内存
一般不关注。
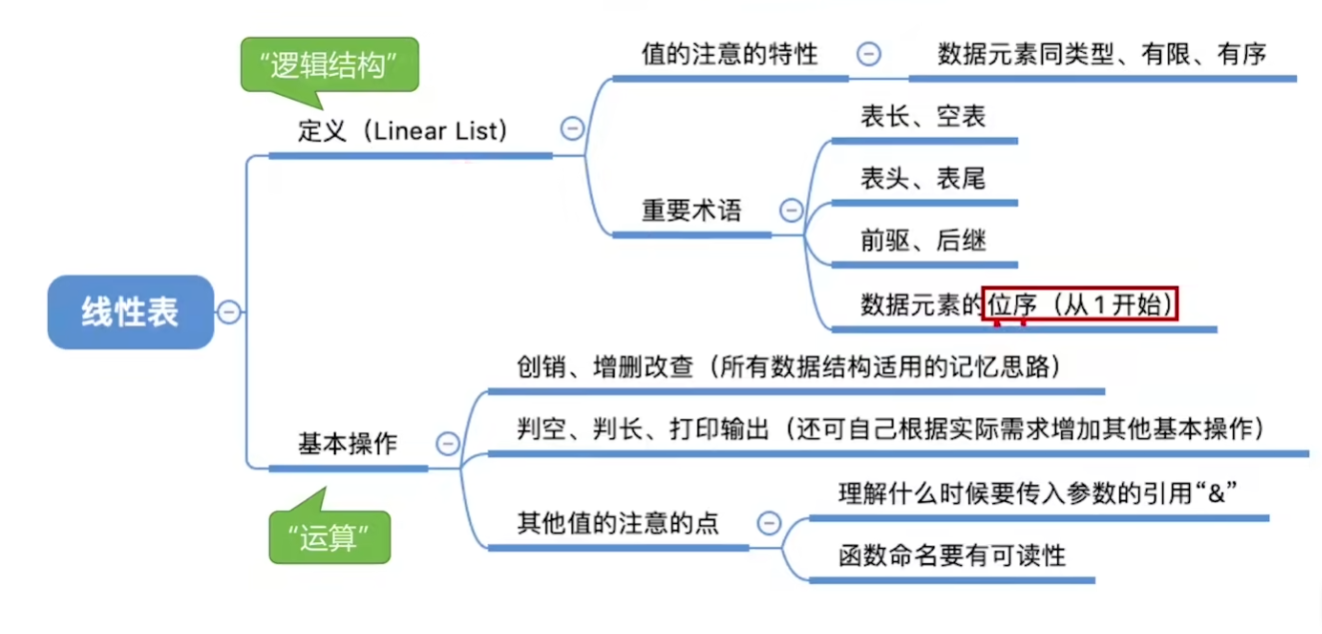
3、线性表
判断方法:如果存在多个元素,且每个元素都有唯一的一个前驱和后继,则该数据结构为线性表。头无前驱,尾无后继。
对数据的操作:增删改查。
1 |
|
这里函数修改了元素值,却没有带回来原因是:传递时,test函数里的x是从main中的x复制过来的,所以修改了x的值,但test函数里的x并没有改变。
如果想将参数的结果带回来,需要传入参数的应用“&”。
团队中,自己定义的数据结构如果要让人很方便的使用,自己就必须进行函数封装,方便调用。避免出错。
3.1、顺序表
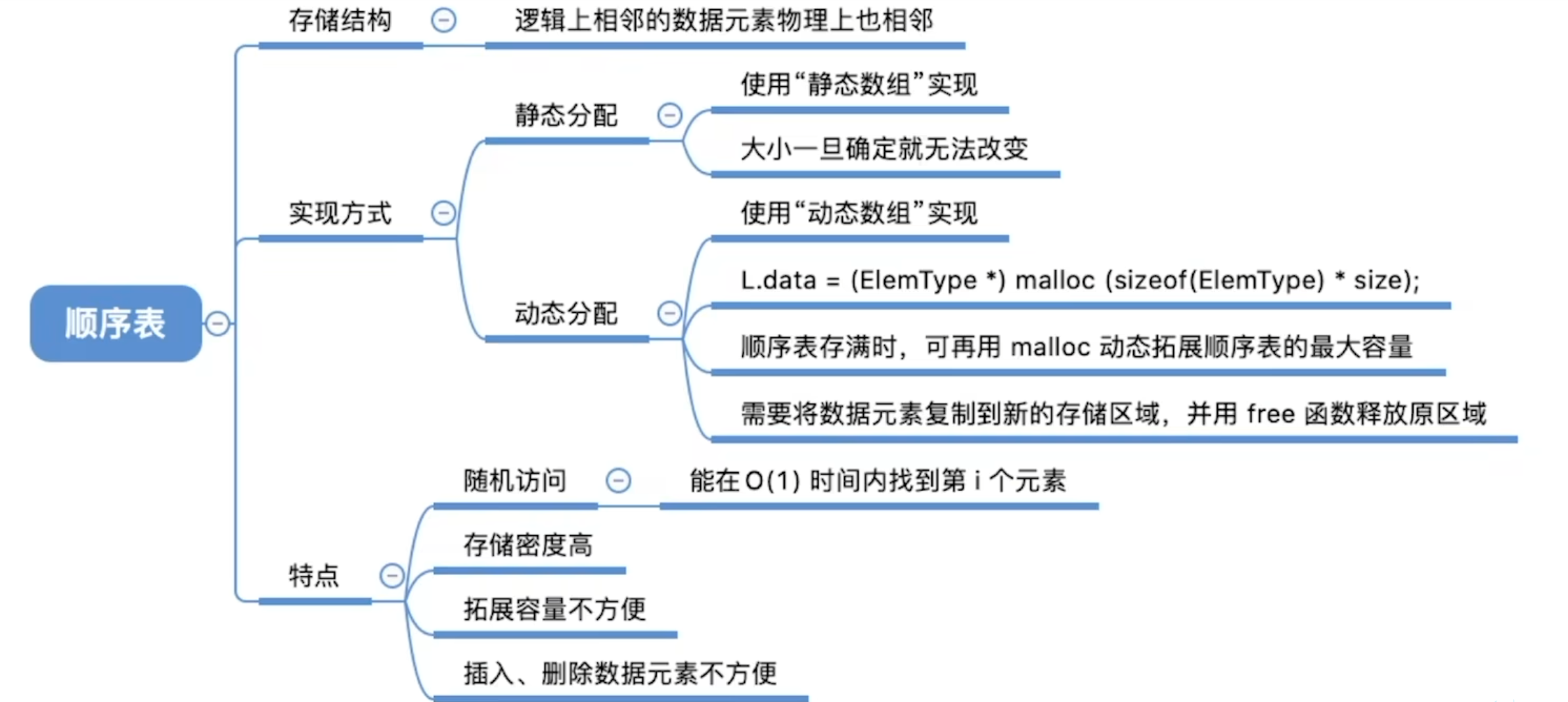
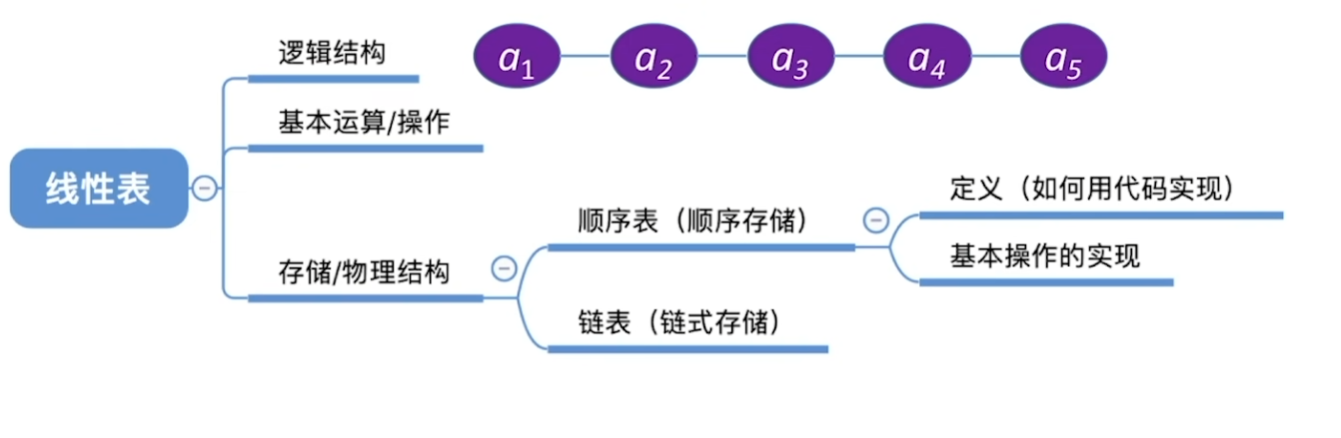
顺序表的实现 – 静态分配
1 |
|
1 |
|
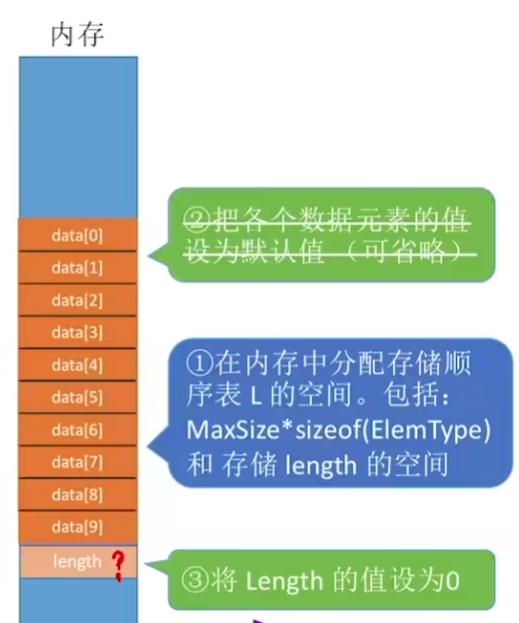
这种分配方式的缺点是:大小无法更改。
就只能采用动态分配的方式。
1 |
|
用c实现
1 |
|
用c++实现
1 |
|
- 顺序表的特点
1、随机访问,时间复杂度为O(1),即通过下标直接访问,效率高。
2、存储密度高,每个节点只存储数据元素。
3、扩展容量不方便(采用动态分配方式实现,时间复杂度较高)。
4、插入、删除操作不方便,需要移动大量的元素。
3-1-2、顺序表的插入
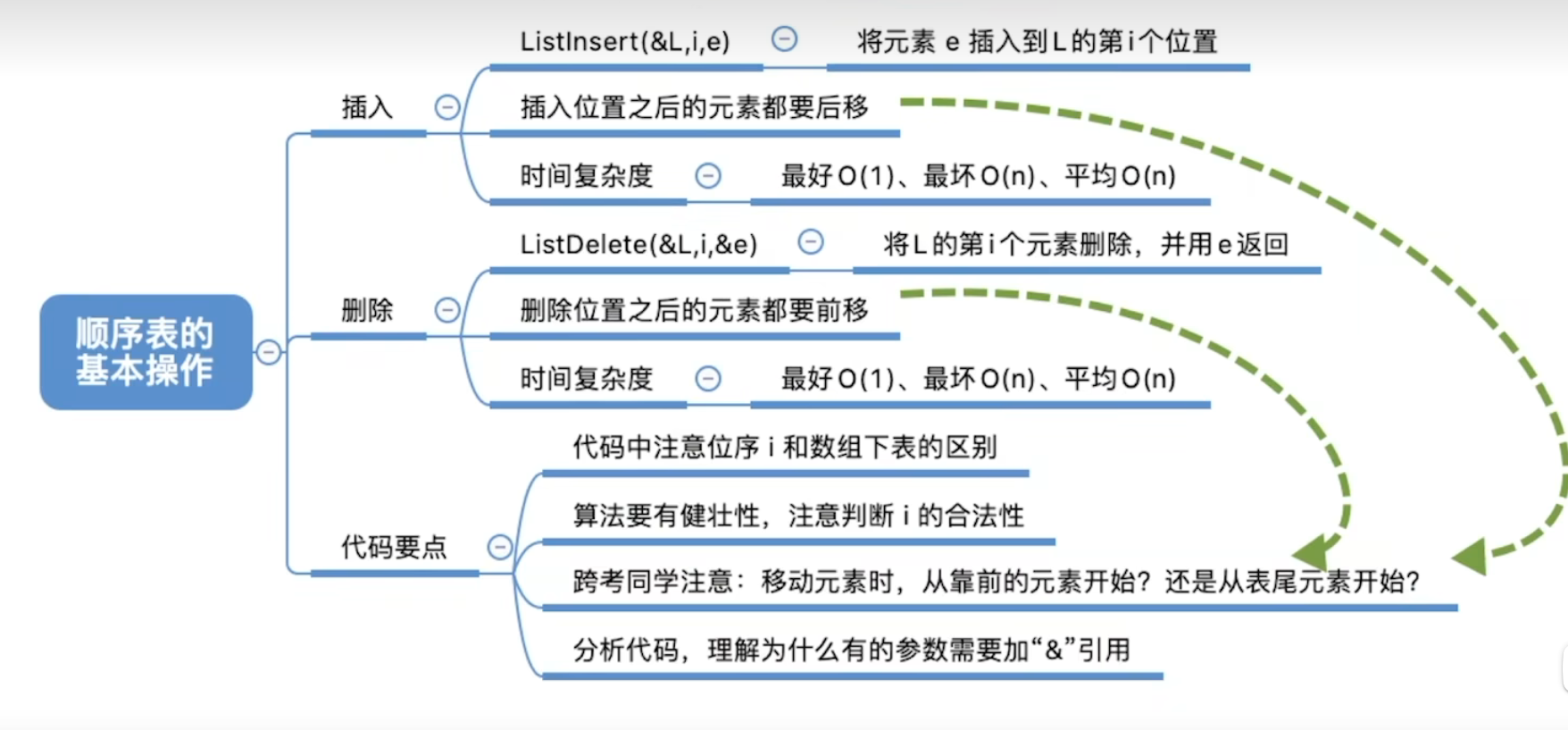
- 顺序表的插入:
1 |
|
顺序表要求插入的时候不能跳跃。
- 时间复杂度情况
最好情况: 插入位置在表尾,时间复杂度为O(1)
最坏情况: 插入位置在表头,时间复杂度为O(n)
平均情况: 插入位置在表中间,时间复杂度为O(n)
- 顺序表的删除
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50bool ListDelete(SqList &L, int i, int &e)
{
if (L.length == 0) return false; // 顺序表为空,不能删除
if (i < 1 || i > L.length) return false; // 位置参数错误
e = L.data[i - 1];
for (int j = i; j <= L.length - 1; ++j) // 删除元素后,将后面的元素全部前移
L.data[j - 1] = L.data[j];
L.length--; // 删除一个元素,表长度减1
return true;
}
int main()
{
SqList L;
Initlist(L);
//...............往顺序表种随便插入几个元素
int e=-1;
if(ListDelete(L, 1, e) == true)
{
cout << "删除的元素为:"<<e;
return 0;
}
else
{
return -1;
}
}
```
函数的传参,需要确定是否需要将参数返回。
不传函数地址或这不取地址,择会重新在内存中复制一份数据。
取地址决定着数据是复制一份还是延用一份。

# 3-1-3、顺序表的查找
* 顺序表的按位查找
getElem(SqList L, int i) // 按位查找操作。获取表L中第i个元素的值。
静态:
```c
typedef struct {
Elemtype data[Maxsize]; // 存储空间
int length; // 表当前的长度
}SqList;
Elemtype getElem(SqList L, int i) // 按位查找操作。获取表L中第i个元素的值。
{
return L.data[i - 1];
}
动态:
1 |
|
对于malloc得到的内存空间。可以采用数组的方式来进行访问。访问方法和访问普通数组一样。
时间复杂度为O(1)。顺序表随机存取。
- 顺序表按照值查找:
LocateElem(SqList L, Elemtype e) // 按值查找操作。获取表L中第1个值为e的元素位置。基本数据类型:int float double char 都可以用==进行比较。1
2
3
4
5
6
7
8
9
10
11
12
13
14
typedef struct {
Elemtype *data; // 存储空间
int maxsize; // 顺序表的最大容量
int length; // 表当前的长度
}SqList;
int LocateElem(SqList L, Elemtype e) // 按值查找操作。获取表L中第1个值为e的元素位置。
{
for (int i = 0; i < L.length; ++i)
if (L.data[i] == e)
return i + 1; // 返回该元素在顺序表中的位置
return 0; // 没有找到
}
时间复杂度:
最坏情况:O(n)
最好情况:O(1)
平均情况:O(n)
3-2、链表
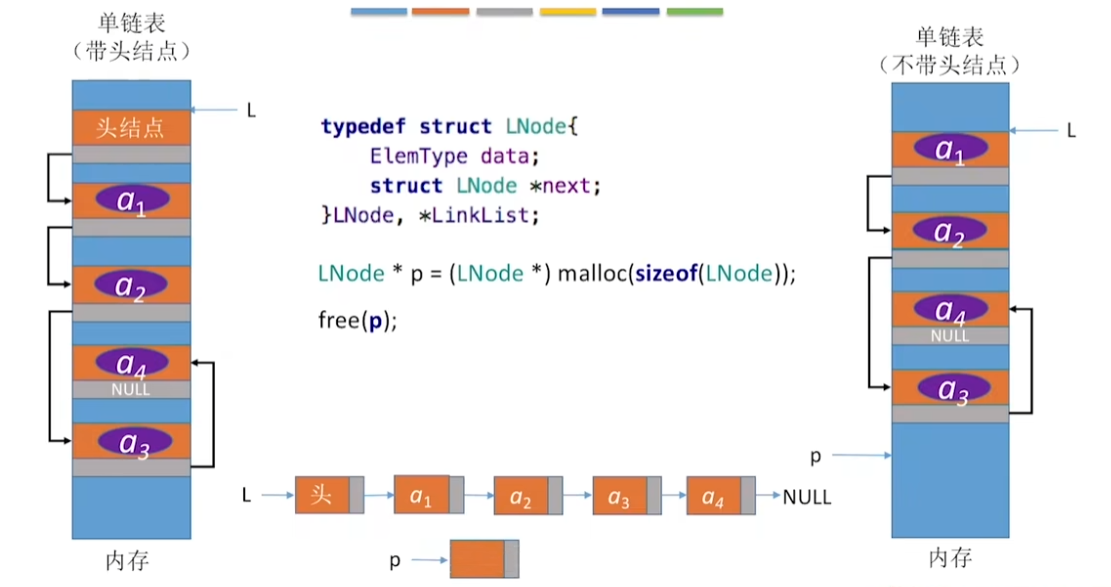
3-2-1、单链表的定义
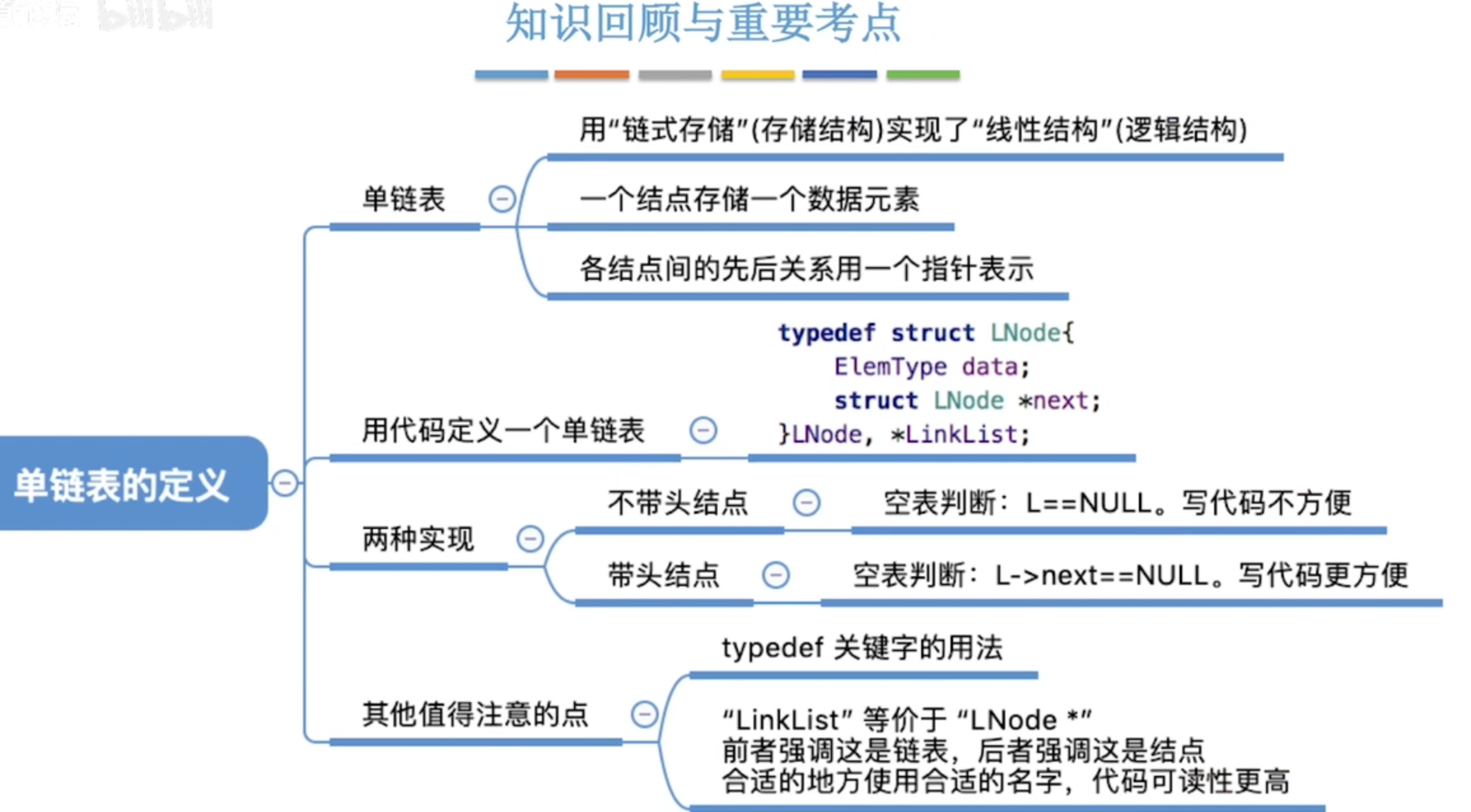
顺序表采用顺序储存,单链表采用链式储存。
1 | typedef struct Node { //节点 |
- 强调这是一个单链表 Linklist
- 强调这是一个节点 Node *
不带头节点的单链表初始化方法:
1 |
|
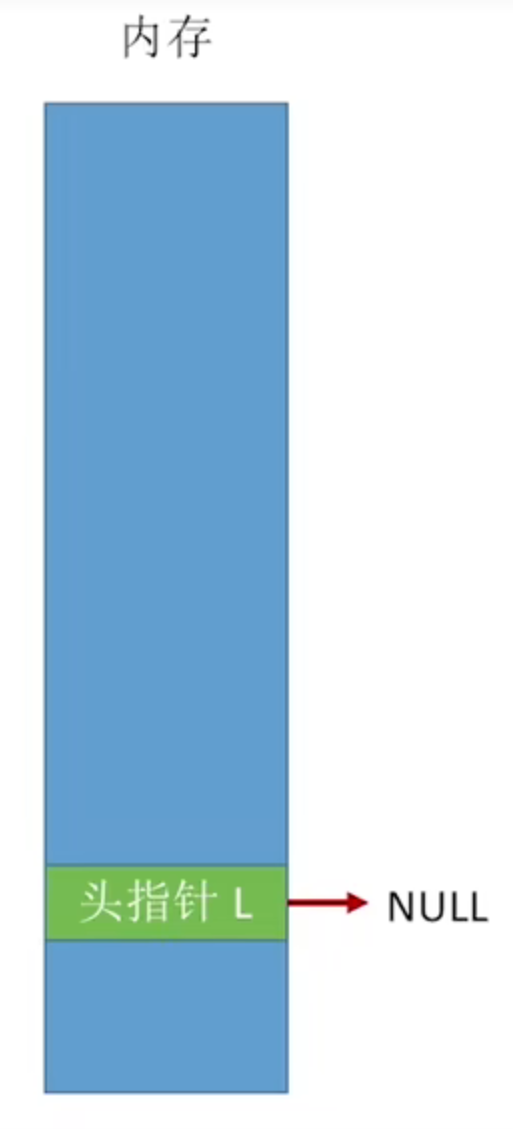
带头节点的单链表初始化方法:
1 | typedef struct Node { |

链表不带头节点,操作比较麻烦。
3-2-2、单链表的插入和删除
- 带头节点(按位序插入)
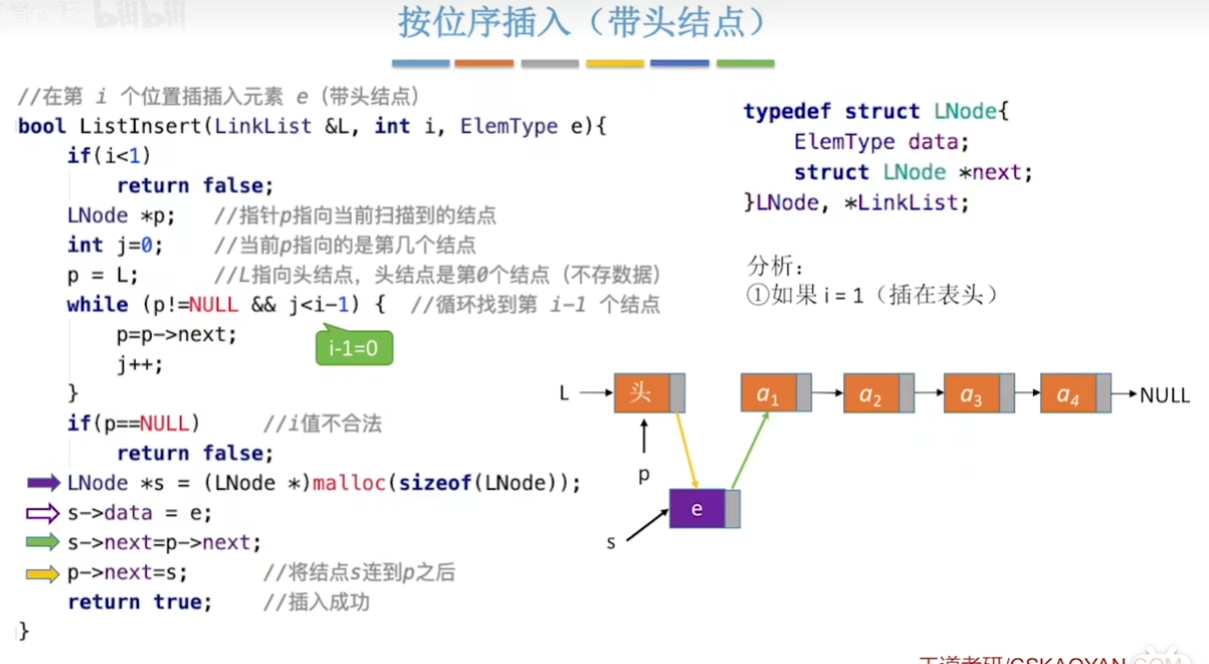
不带头节点(按位序插入)

指定的结点后插入操作
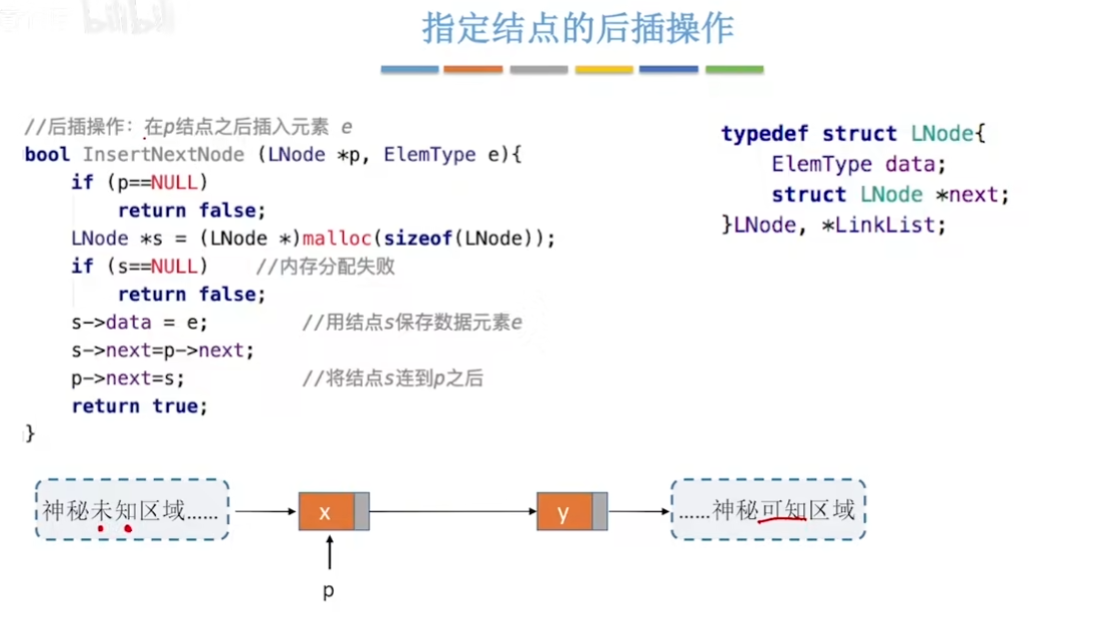
与后面插入操作相比

- 指定节点的前插操作 - 1
1
2
3
4
5bool InsertElem(LinkList L, Node *p,ElemTyep e) //前插操作:在节点p的前面插入值为e的节点 ,L位表头指针
然后遍历插入。
时间复杂度:O(1) - 指定节点的前插操作 - 2 (节点没办法跑路。但是数据可以跑路)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17bool InsertPriorNode(Lnode *p, Elemtype e) // 前插操作:在节点p的前面插入值为e的节点
{
if(p == NULL)
{
return false; // 参数错误,返回false
}
Node *s = (Node *)malloc(sizeof(Node)); // 生成新节点
if (!s)
{
return false; // 内存分配失败,返回false
}
s-next = p->next; // 插入节点
p->next = s; // 将新节点连接到p的后面
s->data = p->data; // 讲p的数据赋值给s
p->data = e; // 将p的数据赋值给e
return true; // 插入成功,返回true
}
.png)
时间复杂度:O(1)
直接传节点方式–原理和带跑数据一样
1 | bool InsertPriorNode(Lnode *p, Node *s) // 前插操作:在节点p的前面插入值为e的节点 |
- 按位序删除(带头节点)
1 | typedef struct Node { |
第二个办法,和带着数据跑插入一样
这次是往要删除的后一个节点的数据赋值到前一个节点,然后删除后一个节点,这样数据就跑到前一个节点了。
1 | bool ListDelete(node *p) // 按位序删除操作, |
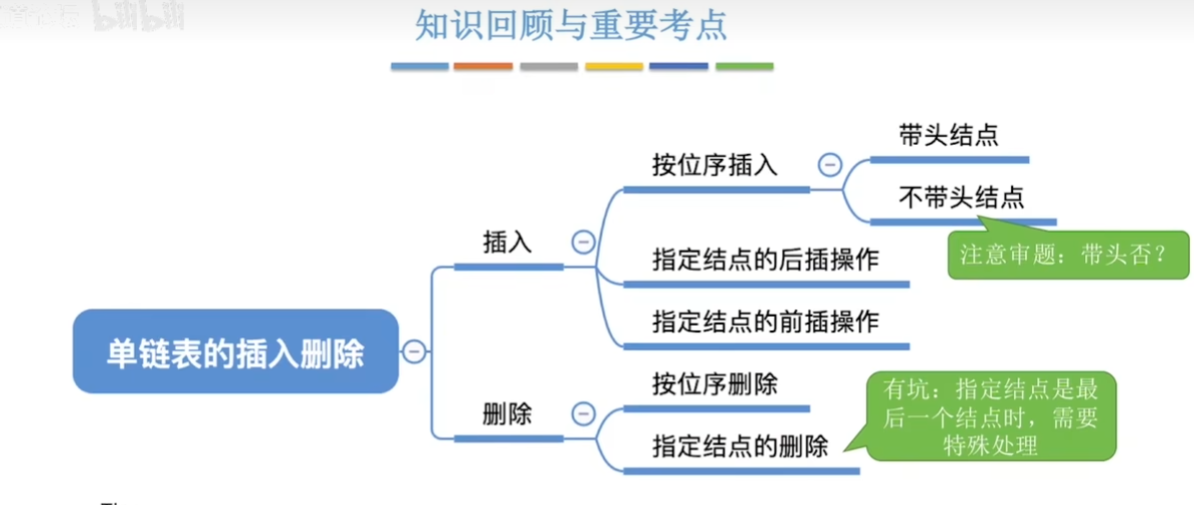
3-2-3、单链表的查找
- 1、按位查找平均时间复杂度:O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/// 按位查找操作,返回第i个结点的数据(带头节点)
Node *GetElem(LinkList L, int i) // 按位序查找操作
{
if(i < 0)
{
return NULL; // 参数错误,返回NULL
}
Node *p; //指针p指向当前扫描到的节点
int j=0; //当前p指向第几个节点
p=L; // 指向头节点
while(p != NULL && j < i) // 找到第i个结点
{
p = p->next; // 指针后移
++j;
}
return p; // 返回第i个结点
}
2、按值查找
1 | /// 按值查找操作,返回值为e的结点(带头节点) |
3-2-4、单链表的建立
3-2-4-1、尾插法
- 方法:创立一个头节点。设置一个指针,永远指向尾节点。尾插法建立单链表:
1
2
3
4
5
6
7
8
9
10
11
12
13
14bool InsertNewElem(Node *p, Elemtype e) // 尾插操作
{
if(p == NULL)
{
return false; // 参数错误,返回false
}
Node *s = (Node *)malloc(sizeof(Node)); // 生成新节点
s->data = e; // 将e赋值给新节点
s->next = p->next; // 将新节点连接到p的后面
p->next = s; // 将新节点连接到p的后面
return true; // 插入成功,返回true
}
初始化链表
设置变量Length记录链表长度
while 循环{
每次取一个数据e
LIstInsert(L, Length++, e);插入尾部
length++
}
3-2-4-2、头插法
方法:对头节点进行后插操作。(元素逆序)
1 | // |
3-2-5、双链表
1 | typedef struct DNode { |
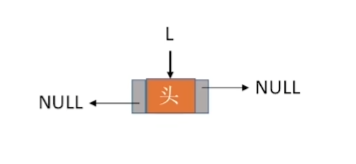
3-2-5-1、双链表的插入
1 | bool ListInsert_DL(DNode *p, DNode *s) // 在p节点后插入s节点 |
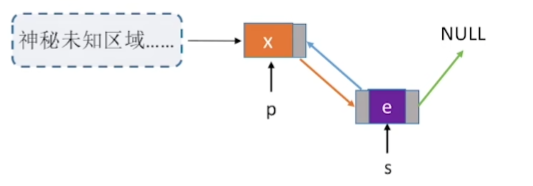
3-2-5-2、双链表的删除
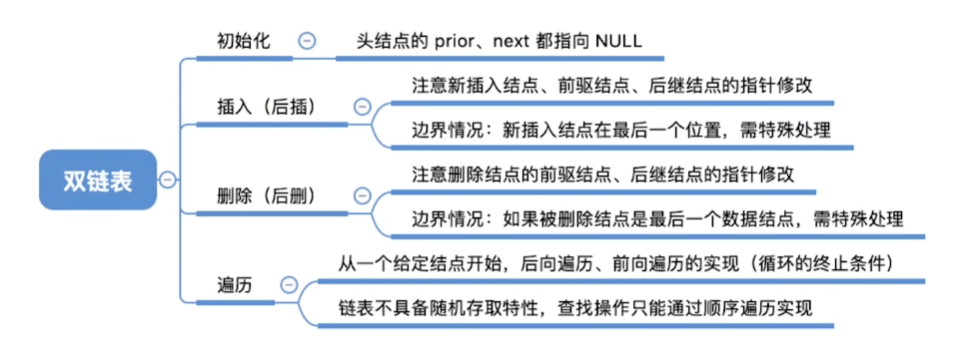
1 |
|
双链表销毁
1
2
3
4
5
6
7
8
9
10
11
12void DestroyList_DL(DLinkList &L) // 销毁操作
{
DNode *p, *q;
p = L->next; // 定义指针p指向头节点
while(p != NULL) // 链表不为空
{
q = p->next; // 定义指针q指向p的后继
free(p); // 释放节点
p = q; // 指针后移
}
L->next = NULL; // 头节点后暂时没有节点
}3-2-5-3、双链表的遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16//向后遍历
while(p != NULL) // 链表不为空
{
p = p->next; // 指针后移
}
//向前遍历
while(p != NULL) // 链表不为空
{
p = p->prior; // 指针后移
}
//向前遍历(跳过带头节点)
while(p->prior != NULL) // 链表不为空
{
p = p->prior; // 指针后移;
}
3-2-6、循环链表
循环链表有两种,循环单链表和循环双链表。
循环单链表常用操作
尾部节点的next指向头节点
- 判断空
1
2
3
4
5
6
7bool Empty_CL(LinkList L) // 判断操作
{
if(L->next == L) // 链表为空,返回true
return true; // 链表为空,返回true
return false; // 链表不为空,返回false
} - 判断是不是表尾节点
1
2
3
4
5
6
7
bool Last_CL(LinkList L, LinkList p) // 判断操作
{
if(p->next == L) // p是尾节点,返回true
return true; // p是尾节点,返回true
return false; // p不是尾节点,返回false
}
循环双链表操作
初始化
1
2
3
4
5
6
7
8
9
10bool InitList_CL(LinkList &L) // 初始化操作
{
L = (Node *)malloc(sizeof(Node)); // 生成头节点
if(!L)
return false; // 内存分配失败,返回false
L->next = L; // 尾节点指向自己
L->prior = L; // 前驱节点指向自己
return true; // 初始化成功,返回true
}判断空
1
2
3
4
5
6bool Empty_CL(LinkList L) // 判断操作
{
if(L->next == L) // 链表为空,返回true
return true; // 链表为空,返回true
return false; // 链表不为空,返回false
}插入
1
2
3
4
5
6
7
8
9
10bool ListInsert_CL(Dnode *p, Dnode *s) // 在p节点后插入s节点
{
if(p == NULL || s == NULL) // 参数错误,返回false
return false;
s->next = p->next; // 将s节点连接到p的后面
p->next->prior = s; //将s节点连接到p的后面
s->prior = p; // 将p节点赋值给s的前驱
p->next = s; // 将p节点赋值给s的前驱
return true; // 插入成功,返回true
}删除
1
2
3
4
5
6
7
8
9
10bool Delete_CL(Dnode *p) // 删除p节点后的q节点
{
if(p == NULL) // 参数错误,返回false
return false;
Dnode *q = p->next; // 定义指针q指向p的后继
p->next = q->next; // 将q节点连接到p的后面
q->next->prior = p; // 将p节点连接到q的后面
free(q); // 释放节点
return true; // 删除成功,返回true
}
3-2-7、静态链表
1 |
|
4、栈
栈:只允许在一端进行插入和删除操作的线性表,后进先出LIFO(Last In First Out)
术语:栈顶top和栈底base,空栈:top == base
基本操作:
1、初始化:分配栈空间
2、销毁:释放栈空间
3、入栈:将元素压入栈顶
4、出栈:将元素从栈顶弹出
5、读栈顶:读栈顶元素
6、判空:判断栈是否为空
4-1、顺序栈
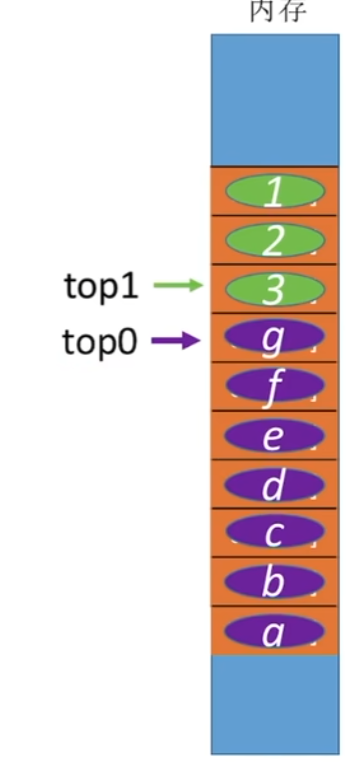
代码中声明结构体,或者变量,就是开辟内存空间
1 |
|
初始化
1
2
3
4void InitStack_Sq(SqStack &S) // 初始化操作
{
S.top = -1; // 栈顶指针置-1
}判空
1
2
3
4
5
6bool Empty_Sq(SqStack S) // 判断操作
{
if(S.top == -1) // 栈为空,返回true
return true; // 栈为空,返回true
return false; // 栈不为空,返回false
}判满
1
2
3
4
5
6bool Full_Sq(SqStack S) // 判断操作
{
if(S.top == MAXSIZE - 1) // 栈满,返回true
return true; // 栈满,返回true
return false; // 栈不满,返回false
}入栈
1
2
3
4
5
6
7bool Push_Sq(SqStack &S, SElemType e) // 入栈操作
{
if(S.top == MAXSIZE - 1) // 栈已满,返回false
return false; // 栈已满,返回false
S.data[++S.top] = e; // 栈顶指针后移,将元素压入栈顶
return true; // 入栈成功,返回true
}出栈
1
2
3
4
5
6
7bool Pop_Sq(SqStack &S, SElemType &e) // 出栈操作
{
if(S.top == -1) // 栈为空,返回false
return false; // 栈为空,返回false
e = S.data[S.top--]; // 栈顶指针前移,将元素弹出
return true; // 出栈成功,返回true
}读栈顶
1
2
3
4
5
6
7bool GetTop_Sq(SqStack S, SElemType &e) // 读栈顶操作
{
if(S.top == -1) // 栈为空,返回false
return false; // 栈为空,返回false
e = S.data[S.top]; // 将栈顶元素赋值给e
return true; // 读栈顶成功,返回true
}
4-1-1、共享栈
1 | typedef struct |
- 初始化内存增长方向相反
1
2
3
4
5void InitStack_Sq(SqQueue &Q) // 初始化操作
{
Q.top0 = -1;
Q.top1 = MAXSIZE;
}
4-2、链栈
使用链表的一段进行插入,或者删除操作,实现栈操作。
5、队列
5-1、顺序队列
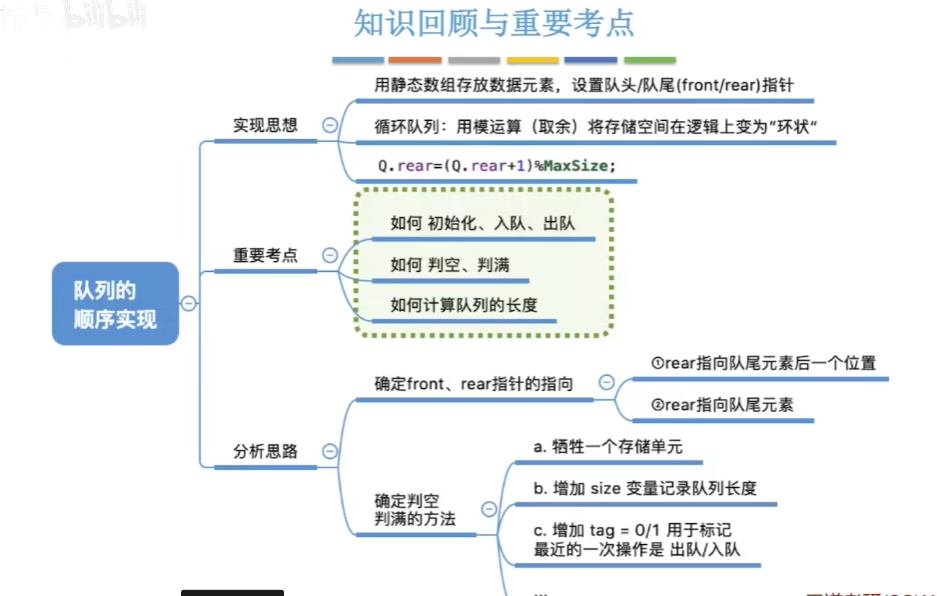
队列:只允许在一端进行插入,在另一端删除的线性表,先进先出FIFO(First In First Out)
术语:队头head和队尾tail,空队列:head == tail
基本操作:
1、初始化:分配栈空间
2、销毁:释放栈空间
3、入队:将元素压入队尾
4、出队:将元素从队首弹出
5、读队首:读队首元素
6、判空:判断栈是否为空
1 |
|
判空
1
2
3
4
5
6bool Empty_Sq(SqQueue Q) // 判断操作
{
if(Q.front == Q.rear) // 队为空,返回true
return true; // 队为空,返回true
return false; // 队不为空,返回false
}入队
1
2
3
4
5
6
7
8bool EnQueue_Sq(SqQueue &Q, SElemType e) // 入队操作
{
if((Q.rear + 1) % MAXSIZE == Q.front) // 队已满,返回false,运用中,会浪费一个存储空间
return false; // 队已满,返回false
Q.data[Q.rear] = e; // 将元素压入队尾
Q.rear = (Q.rear + 1) % MAXSIZE; // 队尾指针后移,相当于一个循环队列
return true; // 入队成功,返回true
}利用取余运算,实现循环队列。逻辑上实现闭环
出队
1
2
3
4
5
6
7
8
9bool DeQueue_Sq(SqQueue &Q, SElemType &e) // 出队操作
{
if(Q.front == Q.rear) // 队为空,返回false,和入队的条件不同,要注意区分
return false; // 队为空,返回false
e = Q.data[Q.front]; // 将队首元素赋值给e
Q.front = (Q.front + 1) % MAXSIZE; // 队首指针后移,相当于一个循环队列
return true; // 出队成功,返回true
}另一种判断队空的方法
1
2
3
4
5
6
7
8
9
typedef struct
{
SElemType data[MAXSIZE]; // 存储空间
int front; // 队首指针
int rear; // 队尾指针
int flag; // 标志位,最后一次是入队还是出队
}SqQueue;
5-2、链队列
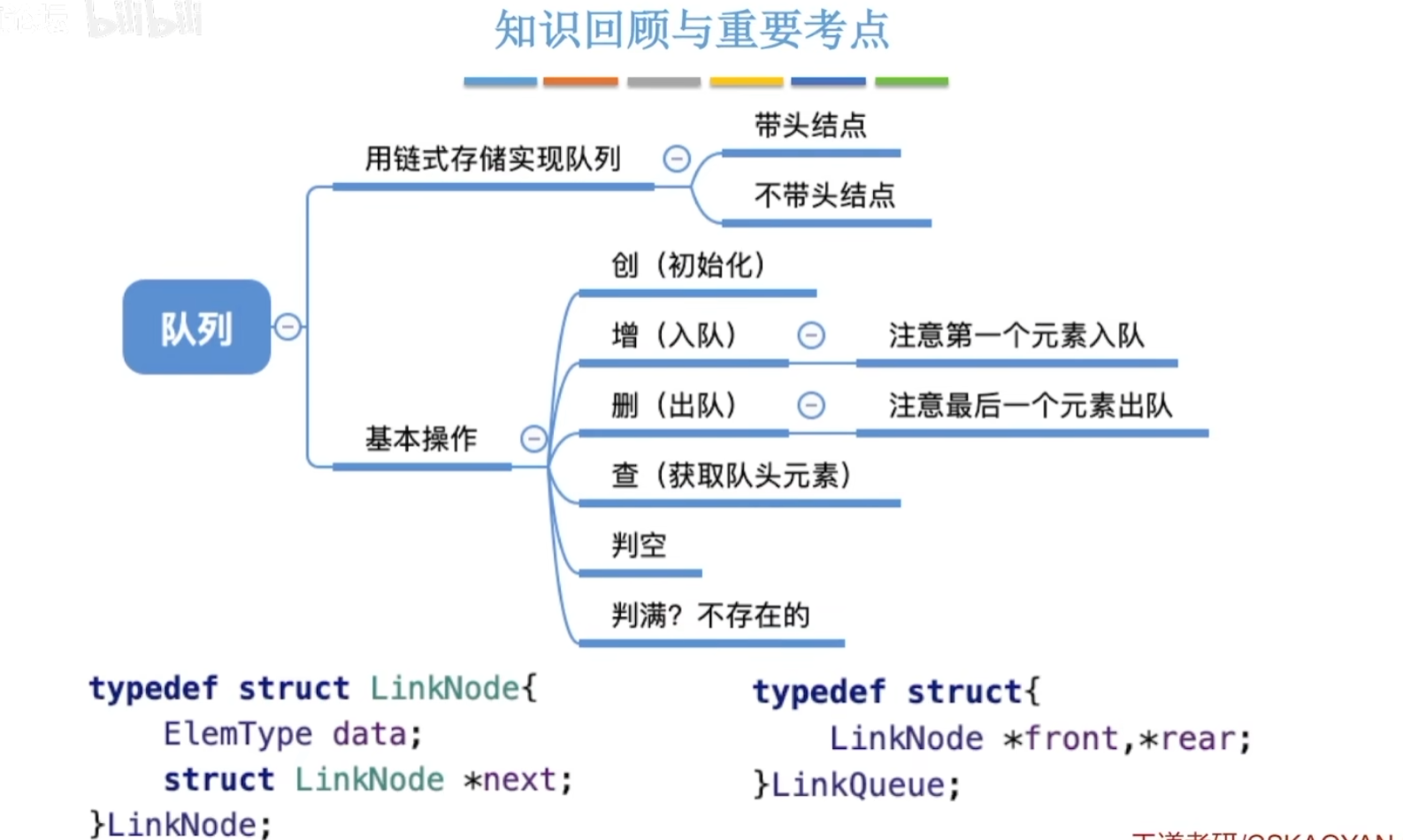
使用链表的一段进行插入,或者删除操作,实现栈操作。
回顾之前的链表,要标记一个链表,只需要保存链表的头指针就可以了。遍历,查询等,这个指针不要动。使用另一个指针,来遍历链表。
- 带头结点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61tyepdef struct QNode
{
SElemType data;
struct QNode *next;
}QNode, *QueuePtr;
typedef struct
{
QNode *front; // 队首指针
QNode *rear; // 队尾指针
}LinkQueue;
/* 初始化 */
bool InitQueue(LinkQueue *Q)
{
Q->front = Q->rear = (QueuePtr)malloc(sizeof(QNode));
if(!Q->front) // 分配失败,返回false
return false; // 分配失败,返回false
Q->front->next = NULL; // 队空,队首指针指向NULL
return true; // 初始化成功,返回true
}
/* 判断空 */
bool IsEmpty()
{
if(Q->front == Q->rear) // 队空,返回true
return true; // 队空,返回true
return false; // 队不空,返回false
}
/* 新元素入队 */
void EnQueue(LinkQueue *Q, SElemType e)
{
QueuePtr s = (QueuePtr)malloc(sizeof(QNode));
if(!s) // 分配失败,返回false
return; // 分配失败,返回false
s->data = e; // 赋值
s->next = NULL; // 队尾指针指向NULL
Q->rear->next = s; // 队尾指针指向新节点
Q->rear = s; // 队尾指针指向新节点
return; // 入队成功,返回true
}
/* 带头节点的链队首元素出队 */
bool DeQueue(LinkQueue *Q, SElemType &e)
{
if(Q->front == Q->rear) // 只有一个元素,
return false; // 头节点,返回false
QueuePtr *p = Q->front->next; // 队首指针
e = p->data; // 队首元素赋值给e
Q->front->next = p->next; // 队首指针指向下一个节点
if(Q->rear == p) // 只有一个元素,队尾指针指向NULL
Q->rear = Q->front; // 只有一个元素,队尾指针指向NULL
free(p); // 释放节点
return true; // 出队成功,返回true
}
void main()
{
LinkQueue Q;
InitQueue(&Q); // 初始化操作
} - 不带头节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54/* 初始化 */
void InitQueue(LinkQueue *Q)
{
Q->front = NULL; // 队空,队首指针指向NULL
Q->rear = NULL; // 队尾指针指向NULL
}
/* 判空*/
bool IsEmpty(LinkQueue Q)
{
if(Q.front == NULL) // 队空,返回true
return true; // 队空,返回true
return false; // 队不空,返回false
}
/* 入队 */
void EnQueue(LinkQueue *Q, QElemType e)
{
QueuePtr s = (QueuePtr)malloc(sizeof(QNode));
if(!s) // 分配失败,返回false
return; // 分配失败,返回false
s->data = e; // 赋值
s->next = NULL; // 队尾指针指向NULL
if(Q->front == NULL) // 队空,队首指针指向新节点
{
Q->front = s;
Q->rear = s; // 队尾指针指向新节点
}
else // 队不空,队尾指针指向新节点
{
Q->rear->next = s;
Q->rear = s; // 队尾指针指向新节点
}
return; // 入队成功,返回true
}
/* 出队操作 */
bbool DeQueue(LinkQueue *Q, QElemType &e)
{
if(Q->front == NULL) // 队空,返回false
return false; // 队空,返回false
QueuePtr p = Q->front; // 队首指针
e = p->data; // 队首元素赋值给e
Q->front = p->next; // 队首指针指向下一个节点
if(Q->rear == p) // 只有一个元素,队尾指针指向NULL
{
Q->rear = NULL; // 只有一个元素,队尾指针指向NULL
Q->front = NULL; // 只有一个元素,队首指针指向NULL
}
free(p); // 释放节点
return true; // 出队成功,返回true
}
5-3、双端队列
有多种形式,双端队列:只允许从两端插入、两端删除的线性表。
输入受限的双端队列:只允许一端插入,两端的删除操作。
输出受限的双端队列:只允许一端删除,两端的插入操作。
6、栈在括号匹配中的应用
IDE:可视化编程环境
1 |
|
7、队列在括号匹配中的应用
表达式:由操作数、运算符和界限符组成的序列。
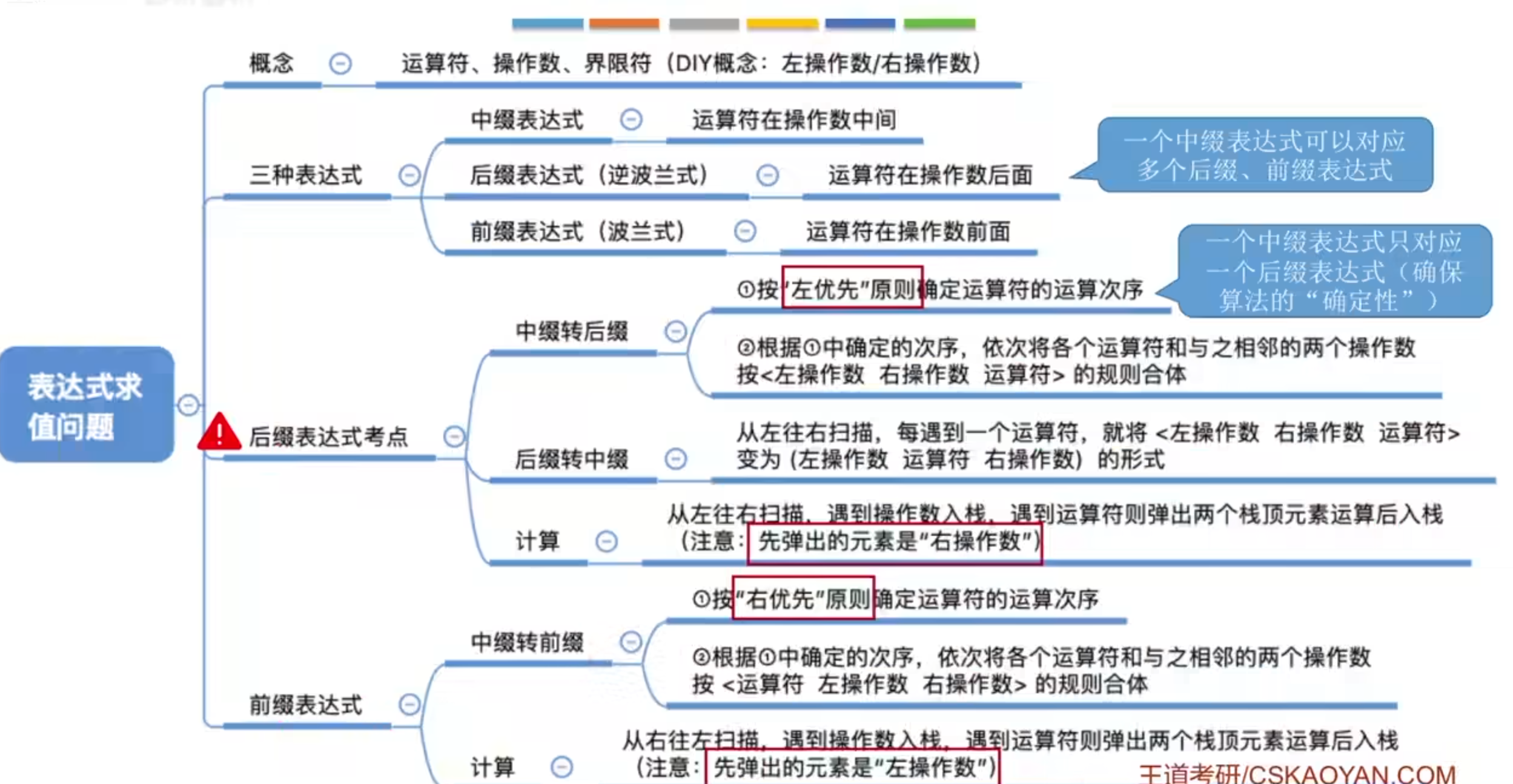

8、栈在递归中的应用
函数调用的特点:最后调用的函数最先返回。也就符合栈的先进后出特点。
函数调用时,需要用栈来保存现场信息。
- 调用返回地址
- 函数参数
- 局部变量
9、队列应用
在操作系统中,进程调度算法:先来先服务、短作业优先、时间片轮转。
在树中,先序遍历、中序遍历、后序遍历。也是用队列来实现的。
10、特殊矩阵的压缩存储
- 一维数组存储结构:线性储存。
- 二维数组存储结构:行优先存储、列优先存储。都是线性。知道行号和列号,能直接得出地址。

- 矩阵:使用数组存储
特殊矩阵:
1、对称矩阵:对角线元素相同。
策略:只存储对角线元素+下三角元素。按行优先存储或者列优先存储。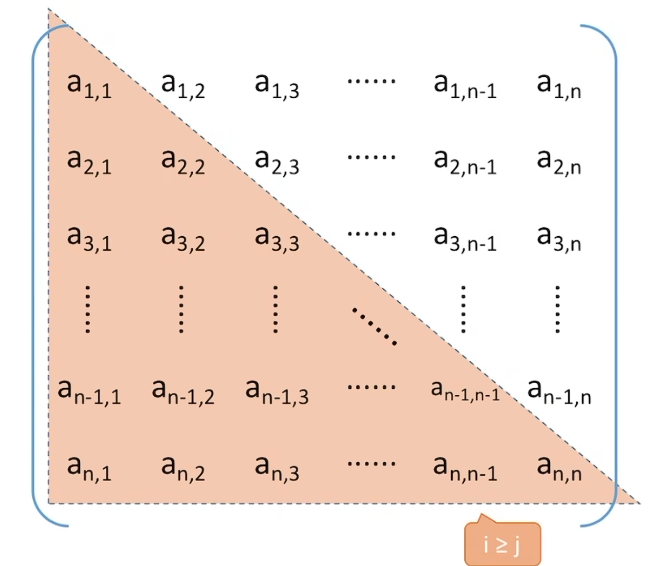
2、三角矩阵:上三角元素和下三角元素都为0。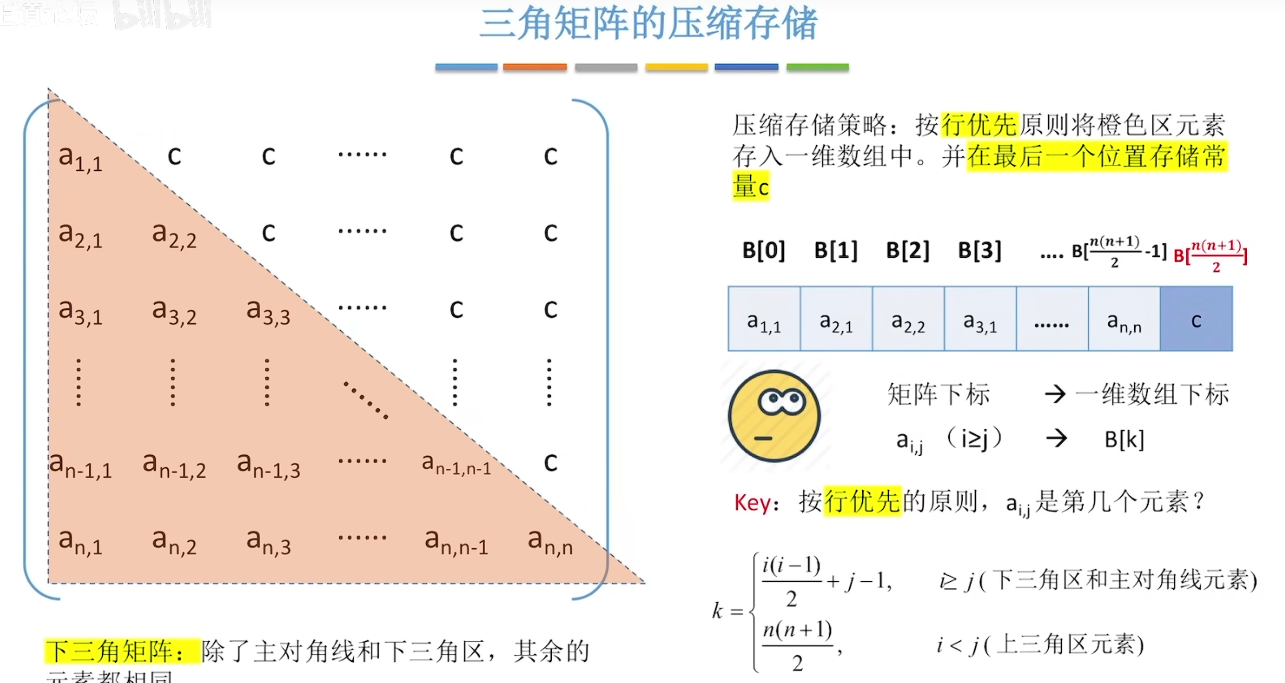
3、对角矩阵:主对角线元素为1,其他元素为0。同样用一维数组存储。
4、稀疏矩阵:元素个数远小于n*m。两种方法存储:顺序存储三元组、链式存储十字链表。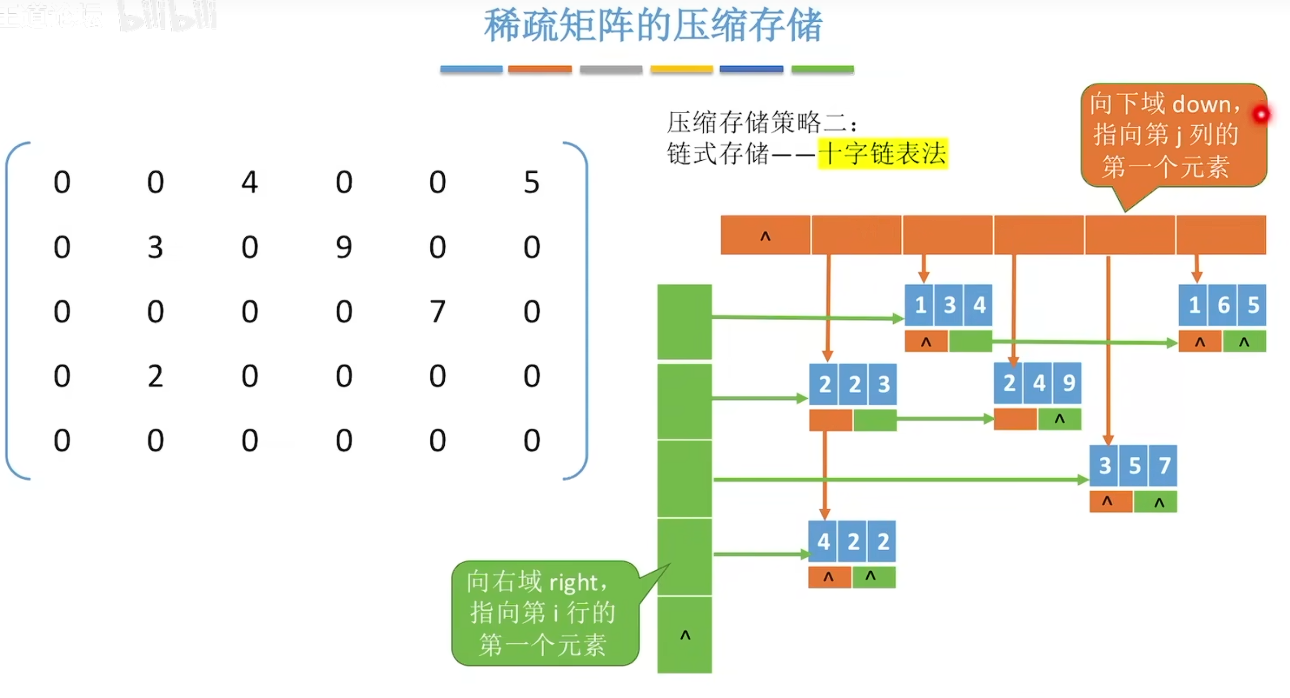
11、串
串:就是字符串,由0个或多个字符组成的有限序列。
串名:字符串的名称,是串的首地址。
串的长度:串中字符的个数。
空串:长度为0的串,空格也算字符。有空格不算空串。
子串:串中任意个连续的字符组成的串。
子串在主串中出现的位置:子串第一个字符在主串中的位置。
存储时以线性的方式存储。
主要操作:
假设有串T=””,S=”iphone 11 pro Max”,W = “pro”
StrAssign(T,s):将串s赋值给串T。
StrEmpty(T):判断串T是否为空串。
StrLength(T):求串T的长度。
StrCopy(T,S):将串S复制给串T。
ClearSring(T):清空串T。
DestoryString(T):销毁串T。
Concat(T,S1,S2):将串S1和S2连接起来,生成新串T。
SubString(&Sub,S,i,j):求子串Sub,其值等于主串S中从第i个字符开始的子串。
Indext(S,T):返回串S中与串T相等的第一个子串的起始位置。否则返回0。
StrCompare(S,T):比较串S和串T的大小关系,逐个字符比较,直到出现大小关系为止。以ASCCII码值大小比较。每个字符的ASCCII码值大小关系。
字符集
- 英文和控制符:ASCCII码值。一个字符占1个字节。
- 中英文:Unicode码值。一个字符占3个字节。
基于同一种码值,不同编码方式,有uft-8、utf-16、utf-32。
11-1、串的存储结构
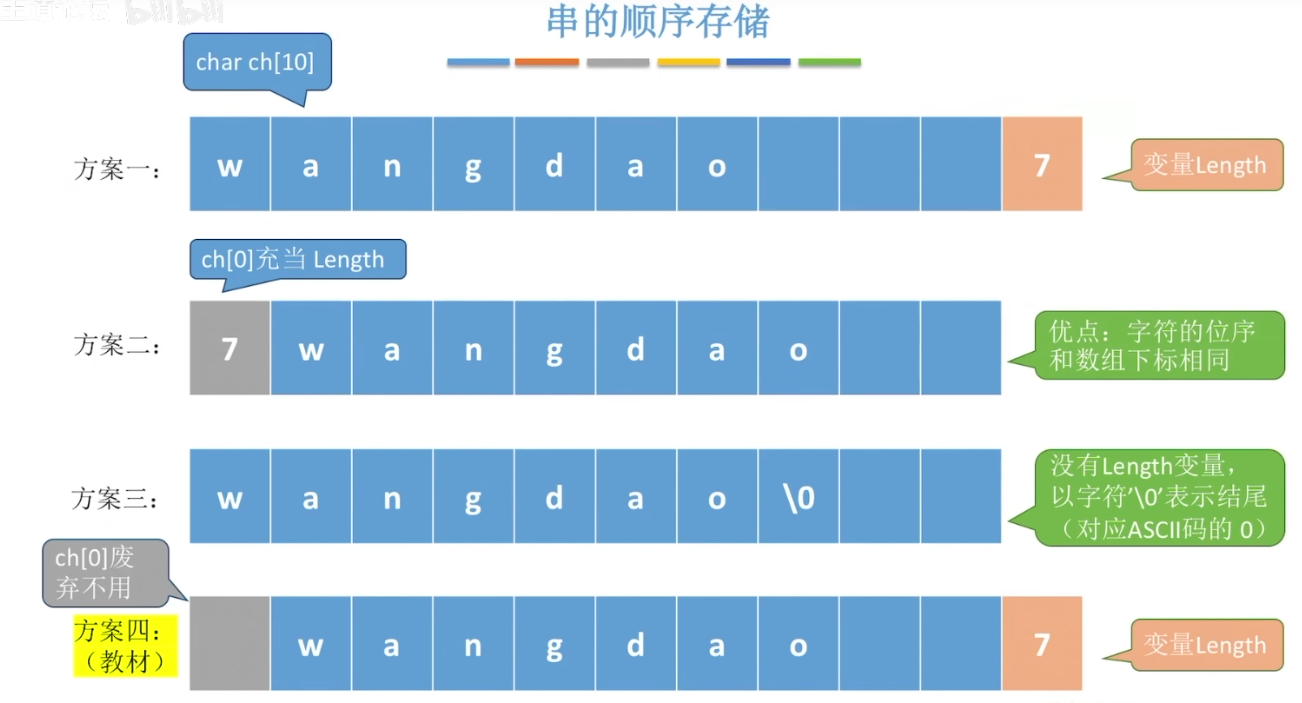
下面11-2采用第四种方法。
顺序存储
1
2
3
4
5
6
typedef struct
{
char data[MAXSIZE]; // 存储空间
int length; // 串的长度
}SqString;顺序存储、堆区
1
2
3
4
5
6
7
8
9
10
typedef struct Node
{
char *ch; // 存储空间
int length; // 串的长度
}LinkNode, *LinkString;
Hstring S;
S.data = (char *)malloc(sizeof(char) * MAXSIZE); // 分配空间
S.length = 0;链式存储
1
2
3
4
5tyoedef struct StringNode
{
char ch[i];//每个节点存储i个字符,提高内存利用率。内存密度。
struct StringNode *next;
}StringNode, *LinkString;
11-2、顺序串的功能实现
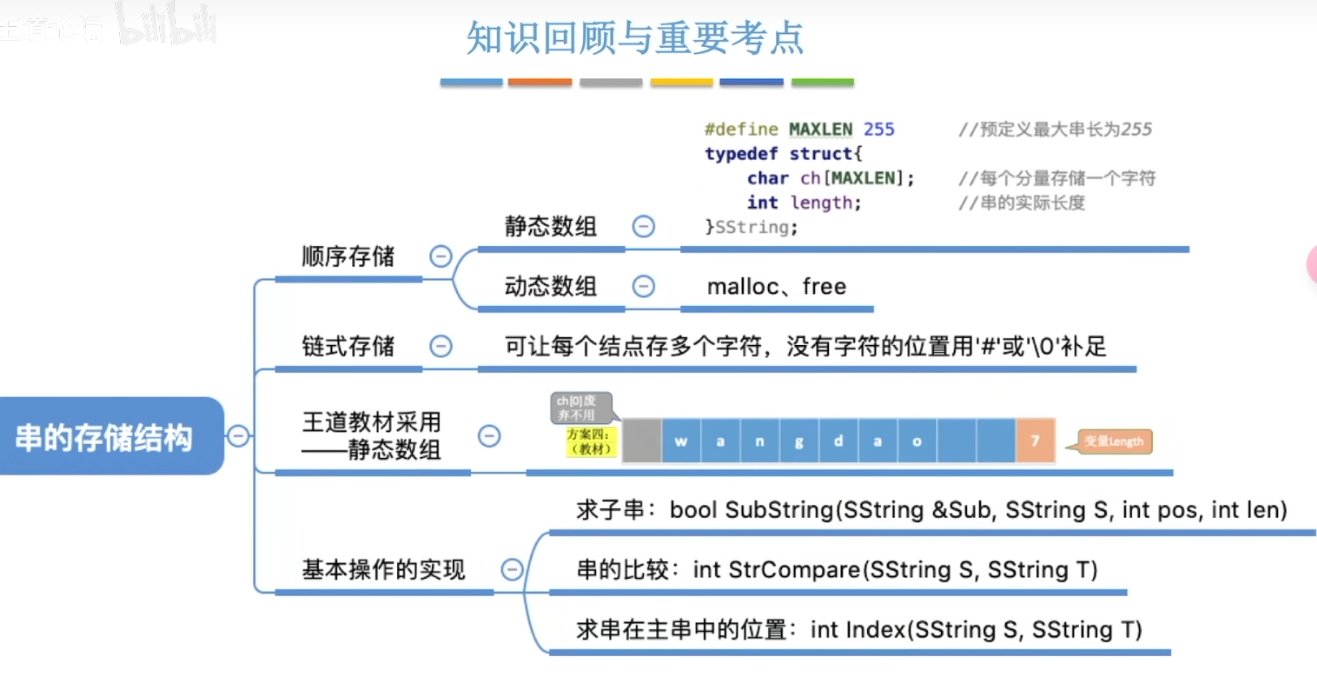
- Substring(&sub,S,i,j):求子串Sub,其值等于主串S中从第i个字符开始,长度为j的子串。
假设S.ch = “yanggguanchao”
S.length = 14
1 |
|
比较串S和串T的大小关系,若S>T,逐个字符比较,直到出现大小关系为止。以ASCCII码值大小比较。
1
2
3
4
5
6
7
8
9int StrCompare(String S,String T)
{
for(int i = 0; i < S.length && i < T.length; i++)
{
if(S.ch[i] != T.ch[i]) // 比较字符ASCCII码值大小
return = S.ch[i] - T.ch[i]; //
}
return S.length - T.length; //
}找子串在主串中出现的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14int Index(String S,String T)
{
int i = 0;
int n = StringLength(S);
int m = StringLength(T);
while(i <= n - m + 1){
Substring(Sub,S,i,m);
if(StrCompare(Sub,T) != 0)
i++;
else
return i; // 返回位置
}
return 0; //S中没有T串
}
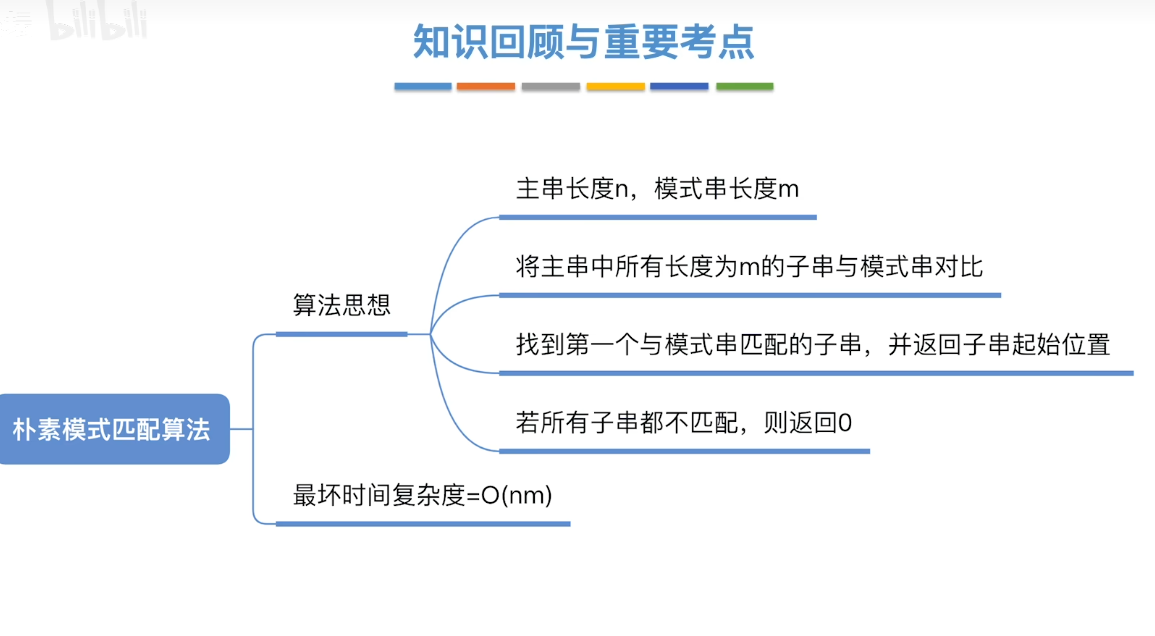
11-3、串的模式匹配
- 朴素模式暴力匹配算法
子串:一定或者没有在主串中
模式串:找到的不一定是你想要的

上一节的子串匹配算法,在主串中找子串。即使一个朴素模式匹配算法。
通过数组下标,进行匹配。主串指针在头处,模式串指针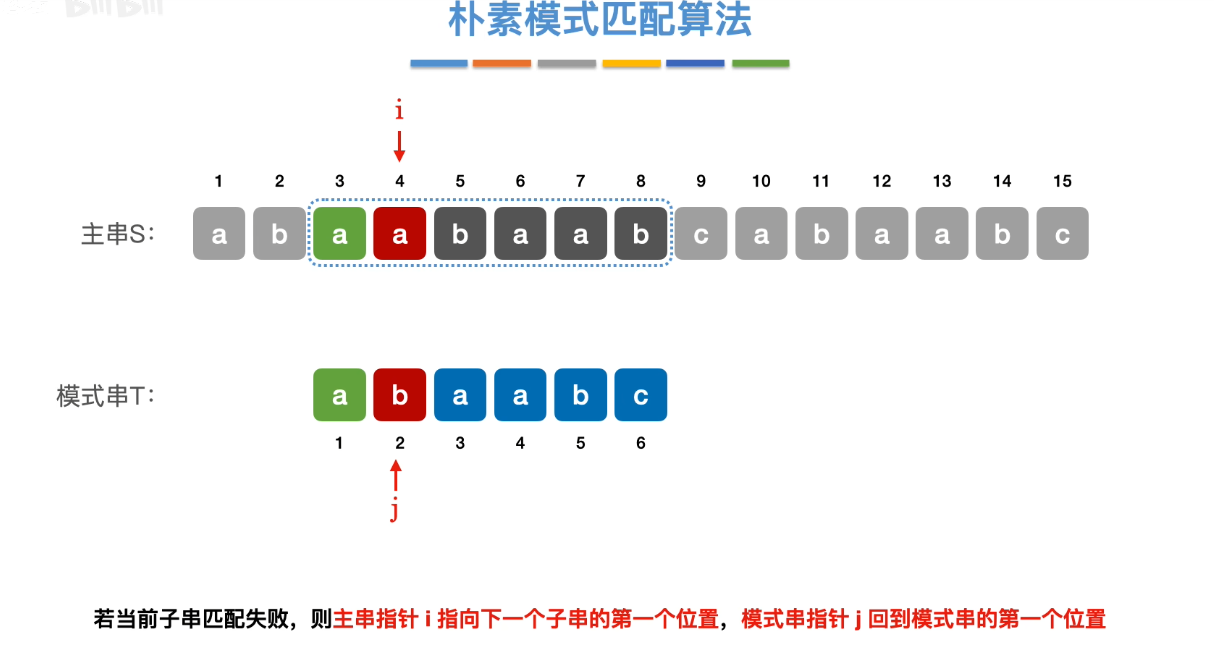
1 | int Index(String S,String T) |
11-4、KMP算法
是对朴素模式匹配算法的改进。主串指针不返回,模式串指针返回
扫描过的位置放到数组中。当发生某一位不匹配,模式串指针返回该位置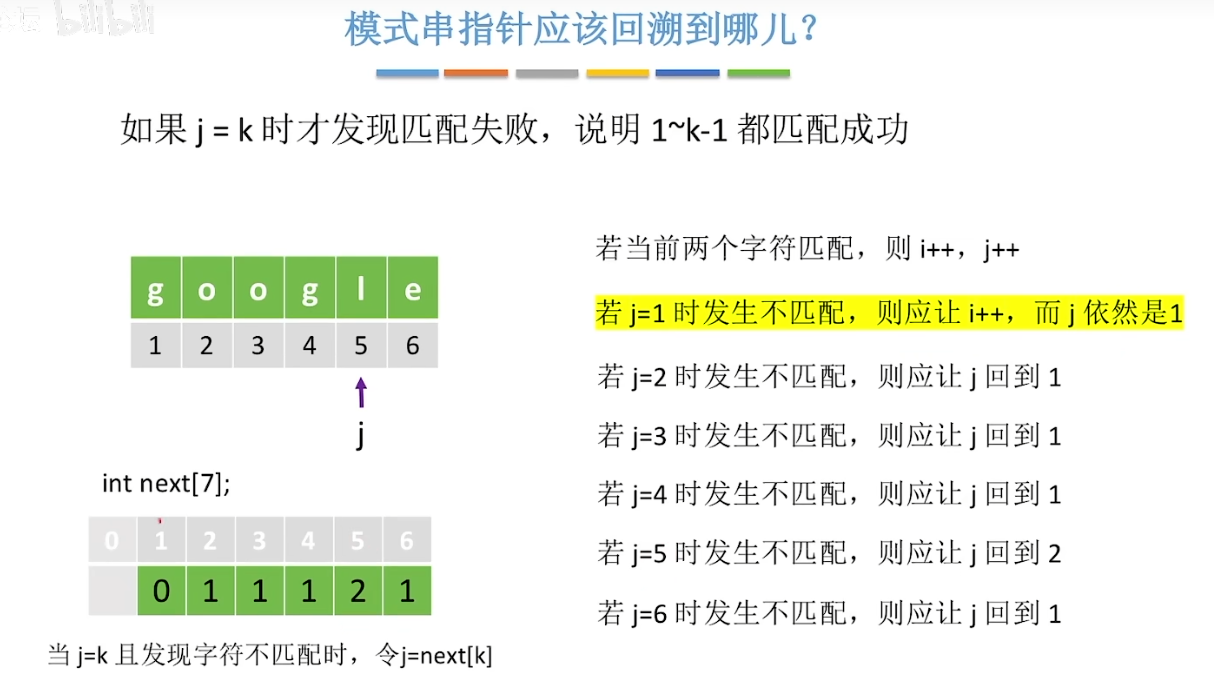
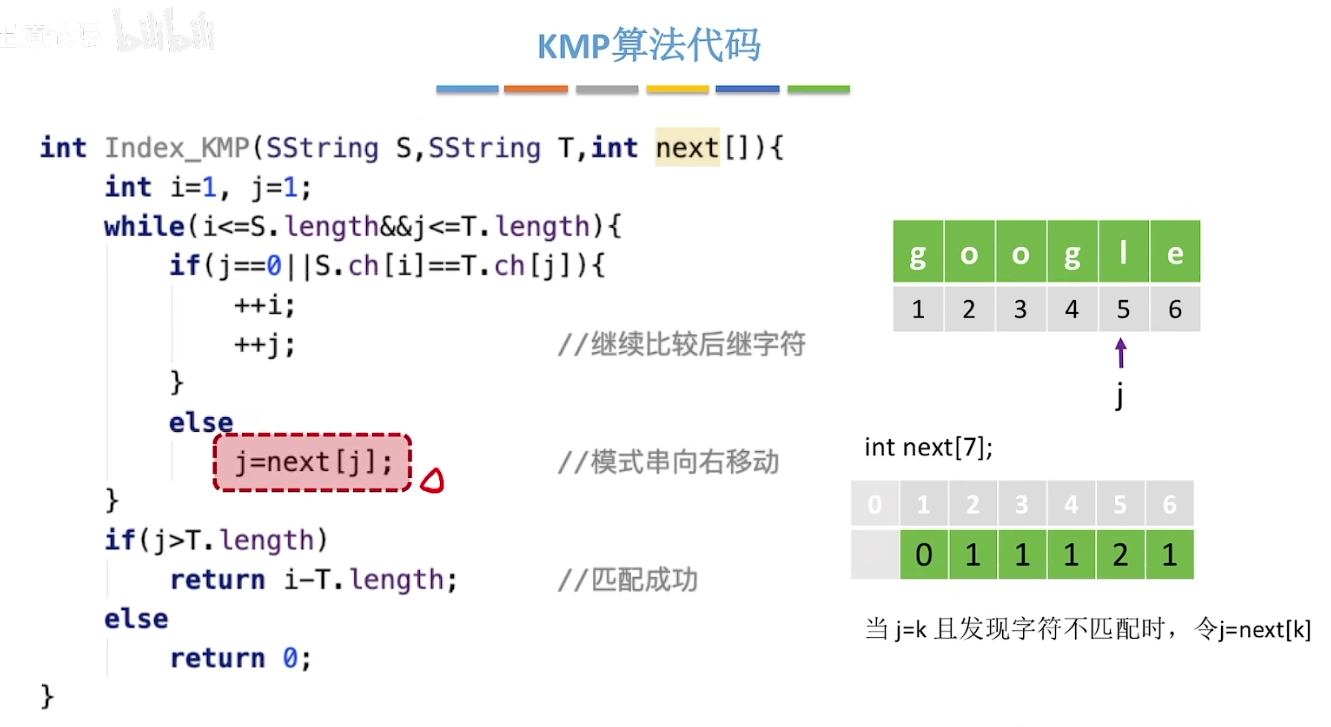
- 求next数组
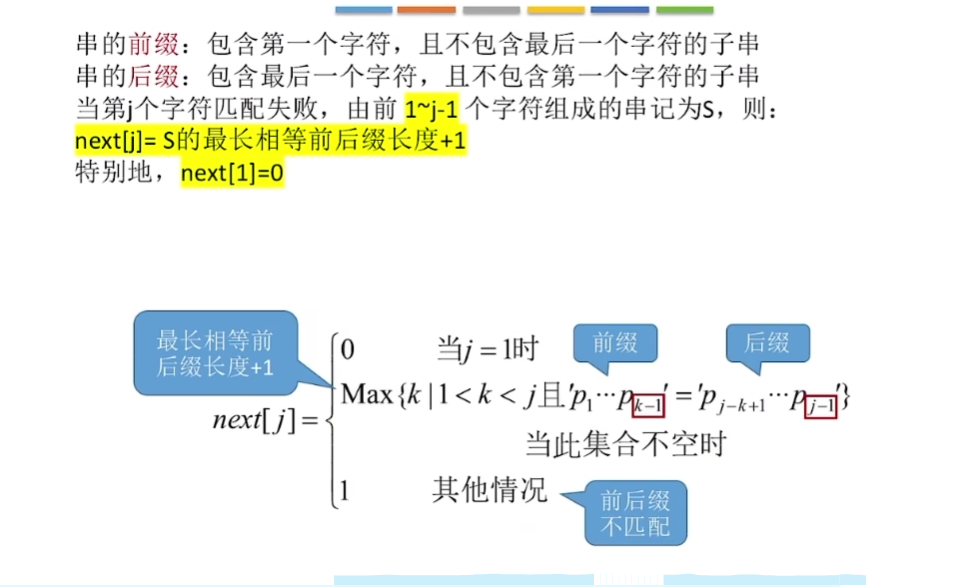
1 | //求模式串T的next数组 |
12、树
根节点:开始节点。
叶子节点:没有子节点的节点。
边:连接节点。
分支节点:有子节点的节点。
空树:没有节点的树。
非空树:
- 有节点的树。有且只有一个根节点。
- 没有后继的节点称之为“叶子节点”
- 有后继的节点称之为“分支节点”
树:由n(n>=0)个节点组成的有限集合。n=0时,称为空树。任意一个非空树m,有且仅有一个根节点。任何一个节点都有仅且只有一个父节点。
树形结构应用
- 文件系统
- 国家省市县区镇村


有序树:从逻辑上看,树中结点的各个子树从左到右是有次序的,不能互换。
无序树:从逻辑上看,树中结点的各个子树从左到右是无次序的,可以互换。

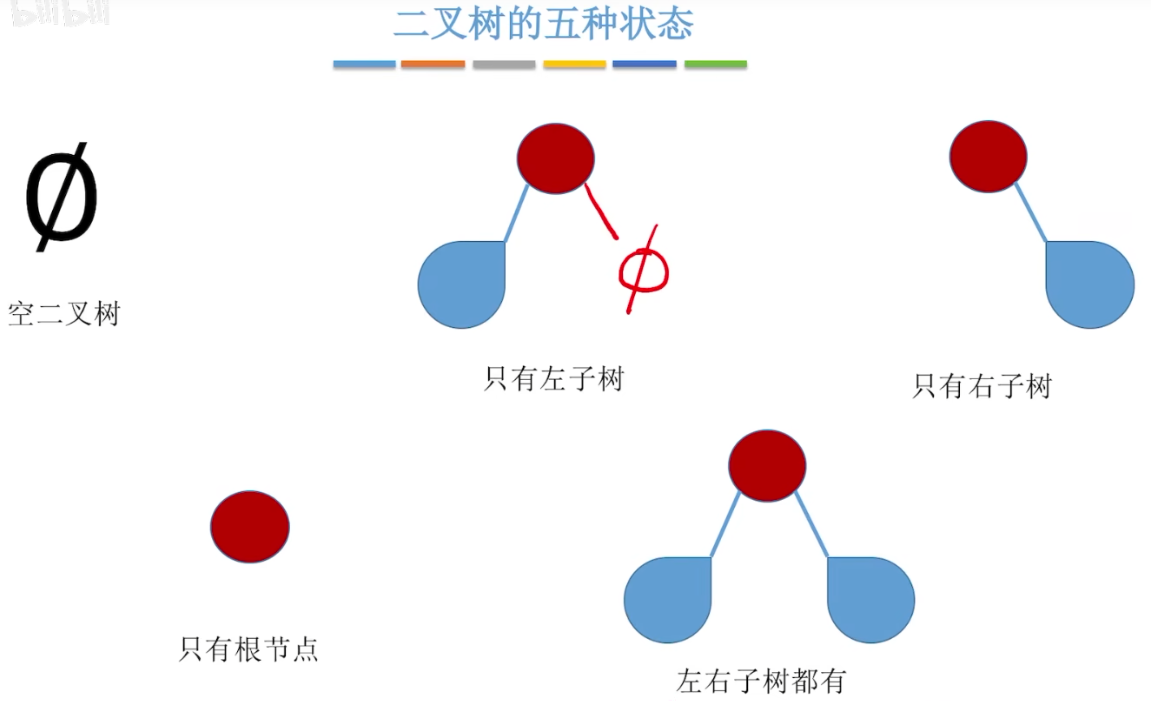
12-1、二叉树
- 定义
二叉树:每个节点最多有两个子树的树结构。 - 二叉树的性质
1、 二叉树的深度为k,则最多有2^k-1个结点。
2、左右树不能互换。有序树。
几种特殊的二叉树:
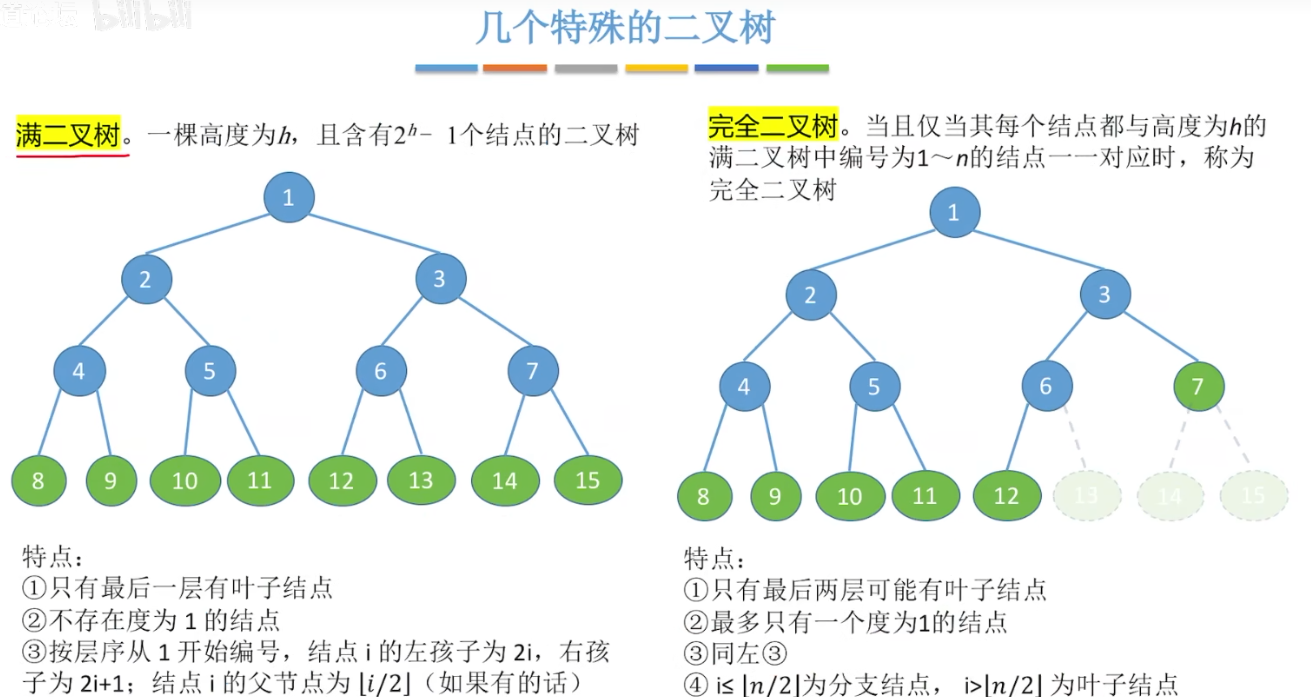
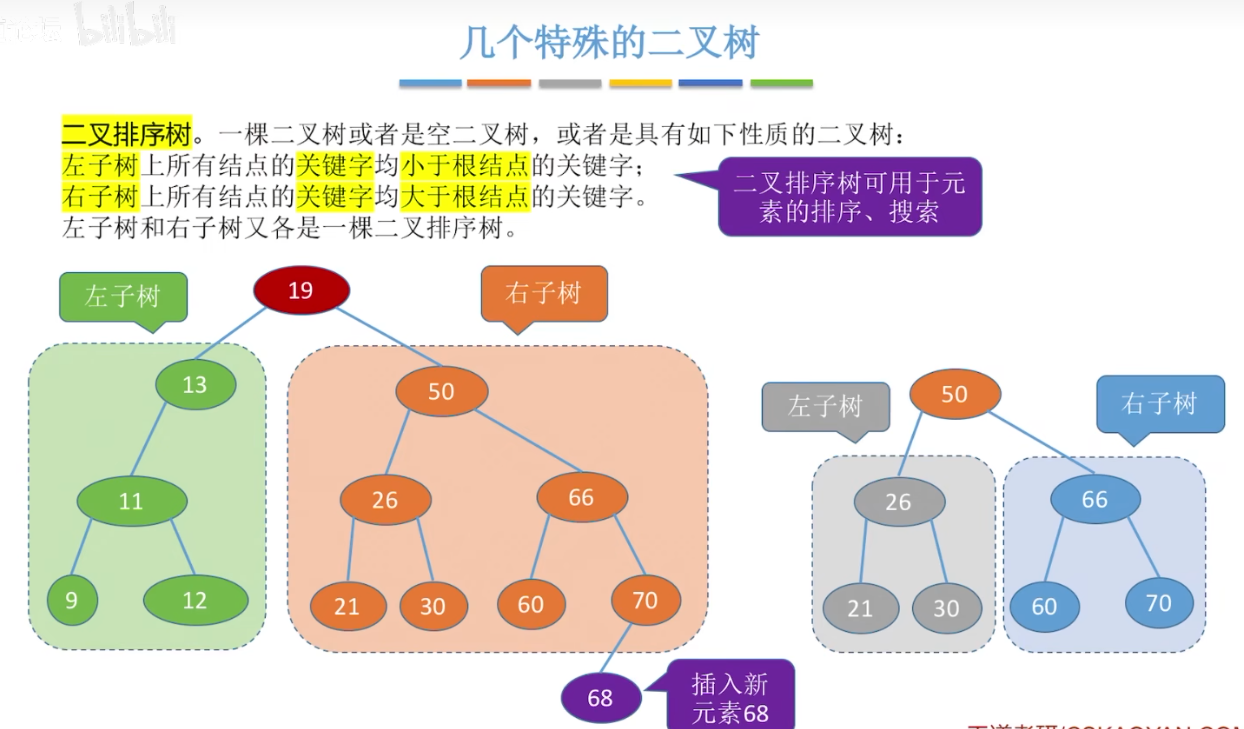
平衡二叉树:左右子树的高度差不超过1。效率很高
12-2、二叉树的存储结构
顺序存储结构:用一维数组存储二叉树。(能快速访问,但是会浪费存储空间)
链式存储结构:用指针域存储二叉树。
1 | //链式存储结构 |
在实际过程中,如果二叉树查找父节点很费时间,可以设置一个指针域,指向父节点。
1
2
3
4
5
6
7 struct BiTNode
{
ElemType data;
结构体指针 left;
结构体指针 right;
结构体指针 parent;
}
12-3、二叉树的遍历

先序遍历:
1、若二叉树为空,则返回空操作;
2、若二叉树非空:
(1)访问根节点;
(2)先序遍历左子树;
(3)先序遍历右子树。
1 | typedef struct BiTNode{ |
中序遍历:
1、若二叉树为空,则返回空操作;
2、若二叉树非空:
(1)中序遍历左子树;
(2)访问根节点;
(3)中序遍历右子树。
1 | void InOrder(BiTree T) |
后序遍历:
1、若二叉树为空,则返回空操作;
2、若二叉树非空:
(1)后序遍历左子树;
(2)后序遍历右子树;
(3)访问根节点。
1 | viod PostOrder(BiTree T) |
12-4、二叉树的层序遍历
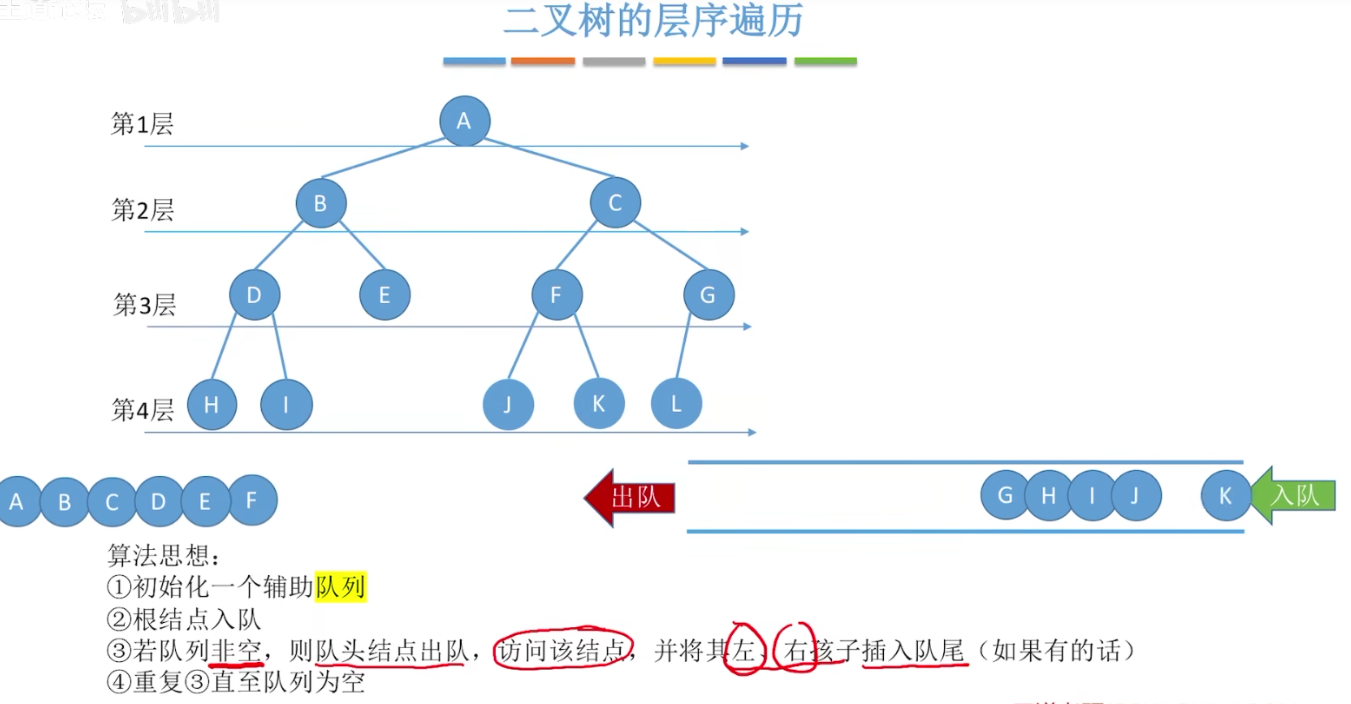
- 算法描述
1、创建一个队列Q,并将根节点入队;
2、根节点入队后
3、若队列非空,则队头元素出队,访问该节点;并判断该节点的左右孩子是否为空,若非空,则将该节点入队;
4、循环3,直到队列为空。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void LevelOrder(BiTree T)
{
LinkQueue Q;//创建队列
InitQueue(&Q);//初始化队列
BiTree p;
EnQueue(&Q, T); //根节点入队
while(!QueueEmpty(Q))
{
DeQueue(&Q, &p); //队头元素出队
visit(p); //访问该节点
if(p->lchild != NULL)
EnQueue(&Q, p->lchild); //左孩子入队
if(p->rchild != NULL)
EnQueue(&Q, p->rchild); //右孩子入队
}
return;
}
12-5、根据几种遍历序列重建二叉树
中序遍历序列和其他三种方式任意结合一种,都可以唯一确定一棵二叉树。
但是不用中序遍历,其他两种结合无法确定一棵二叉树。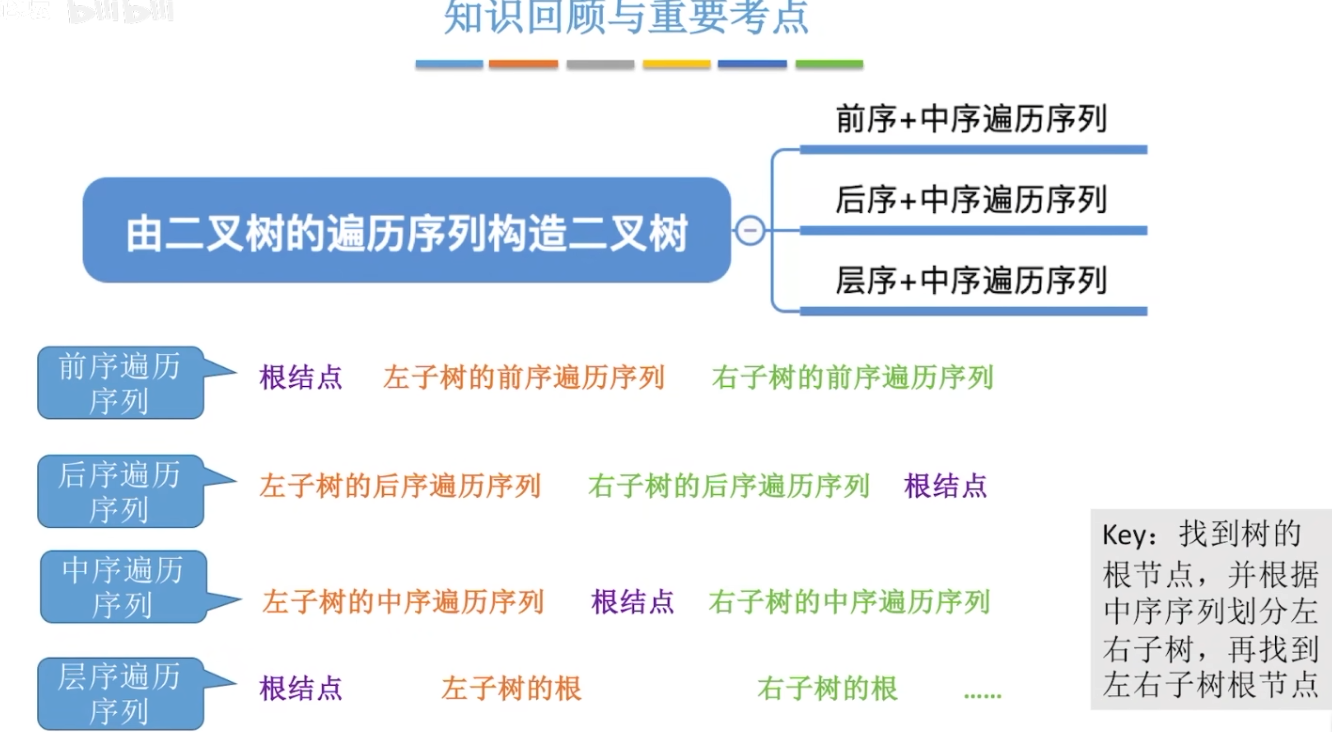
12-6、线索二叉树
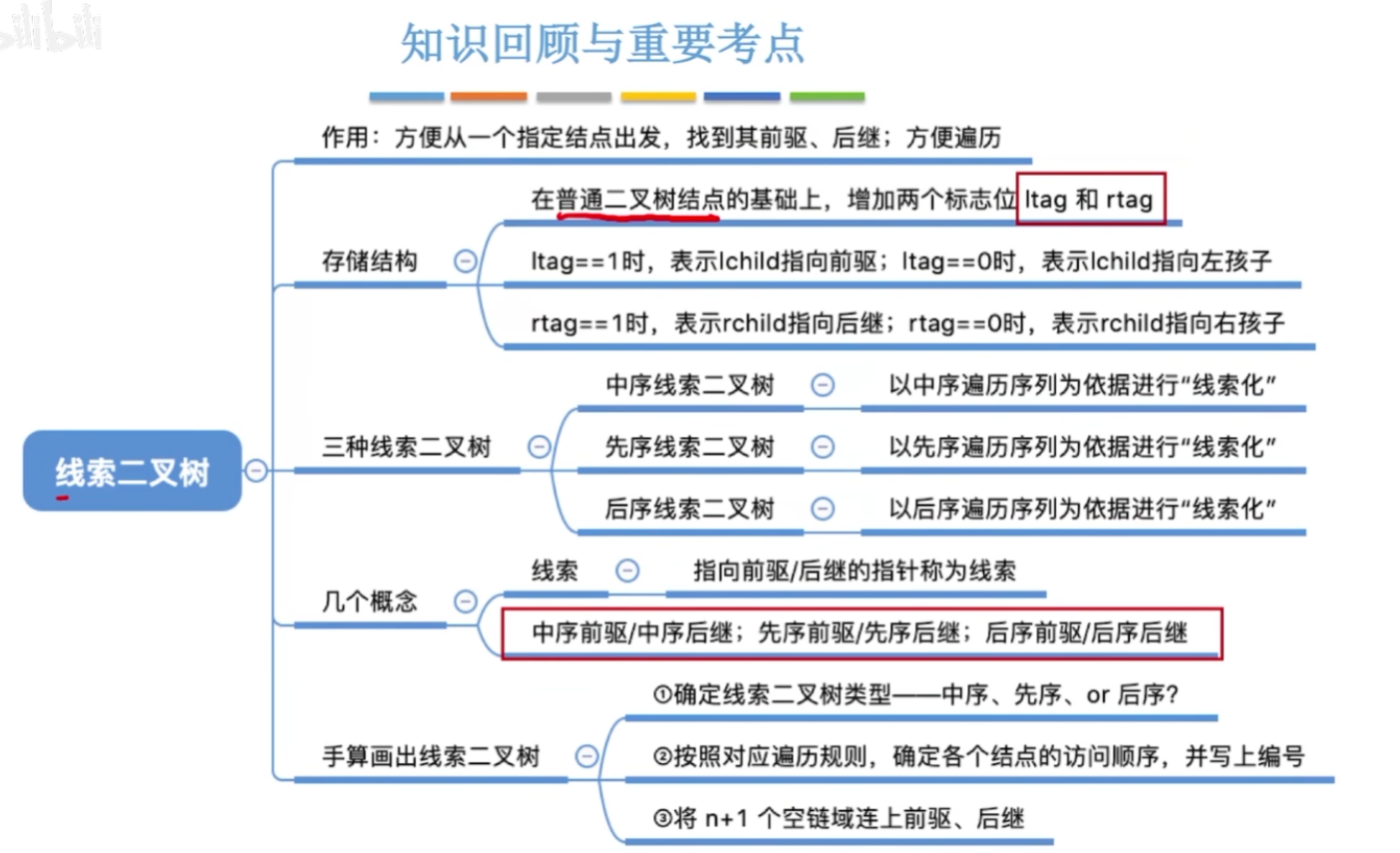
普通二叉树找前驱后继比较麻烦。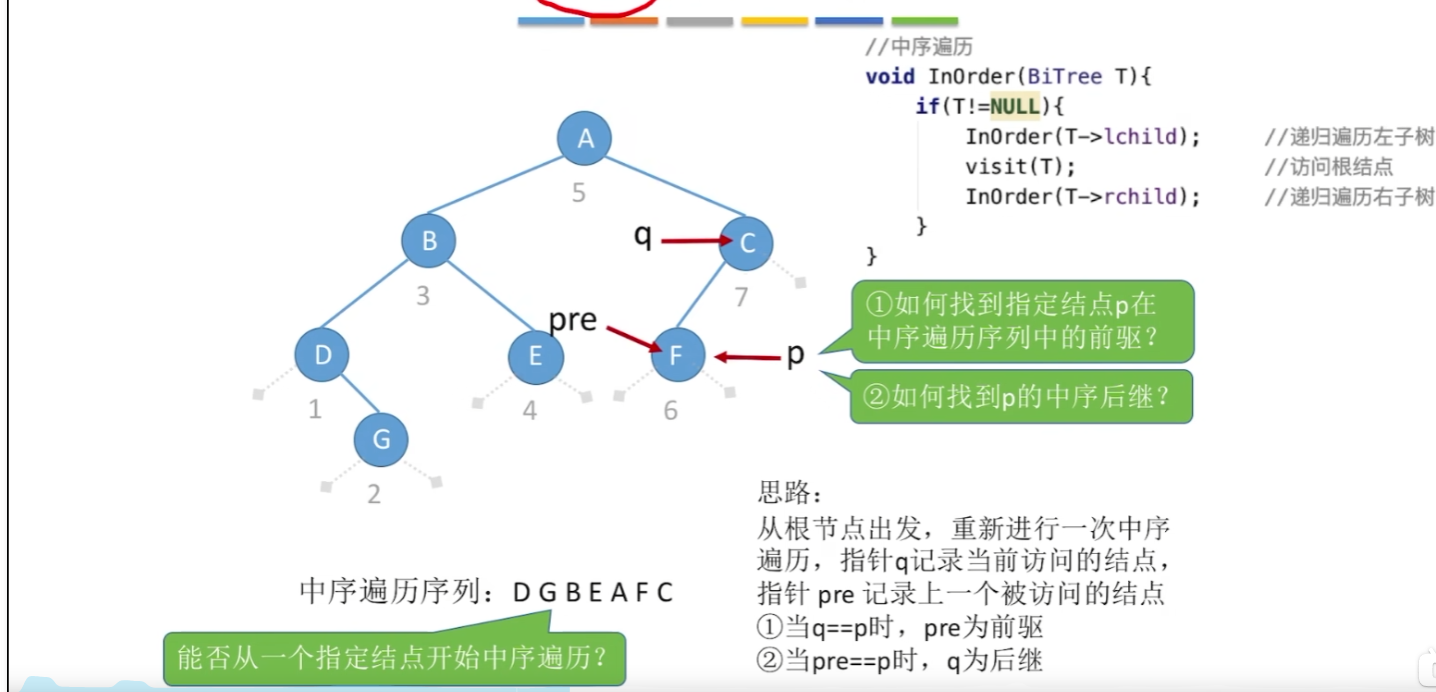
1 | // 创建线索二叉树 |
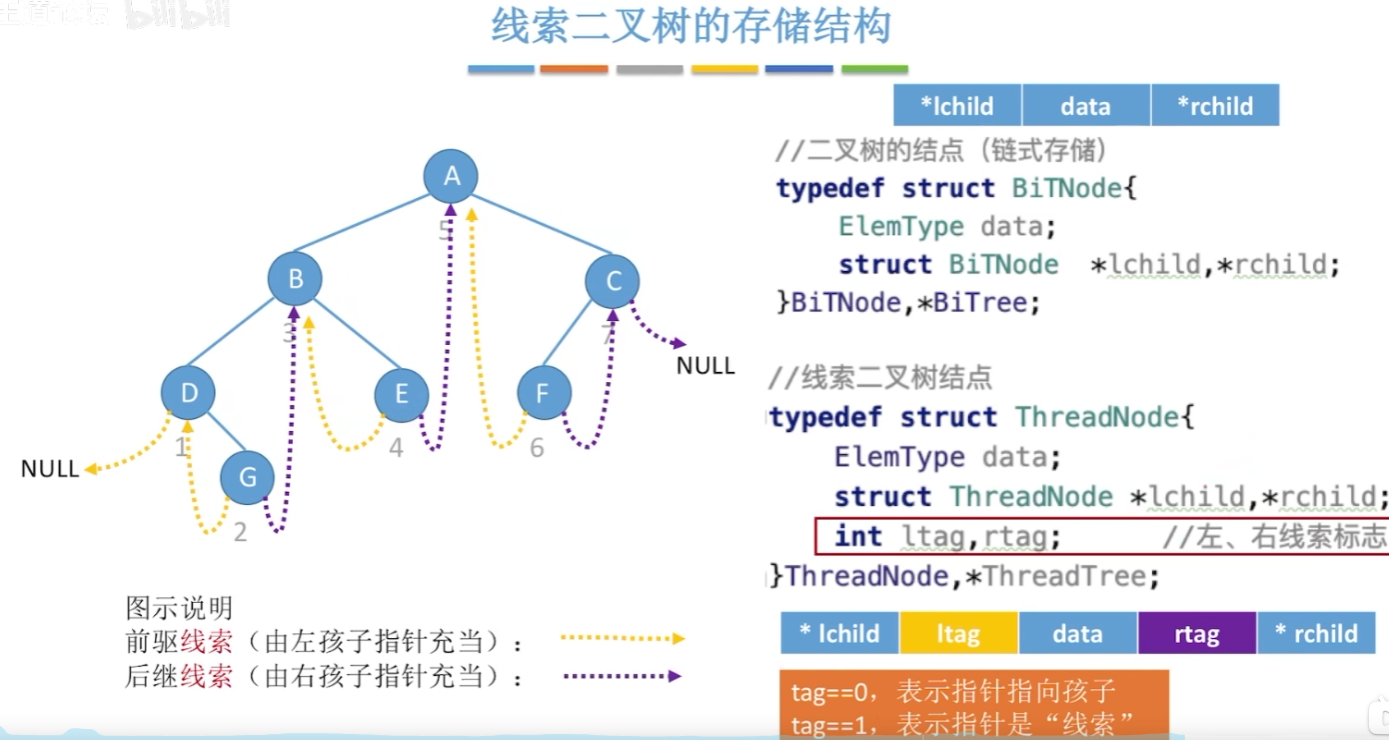
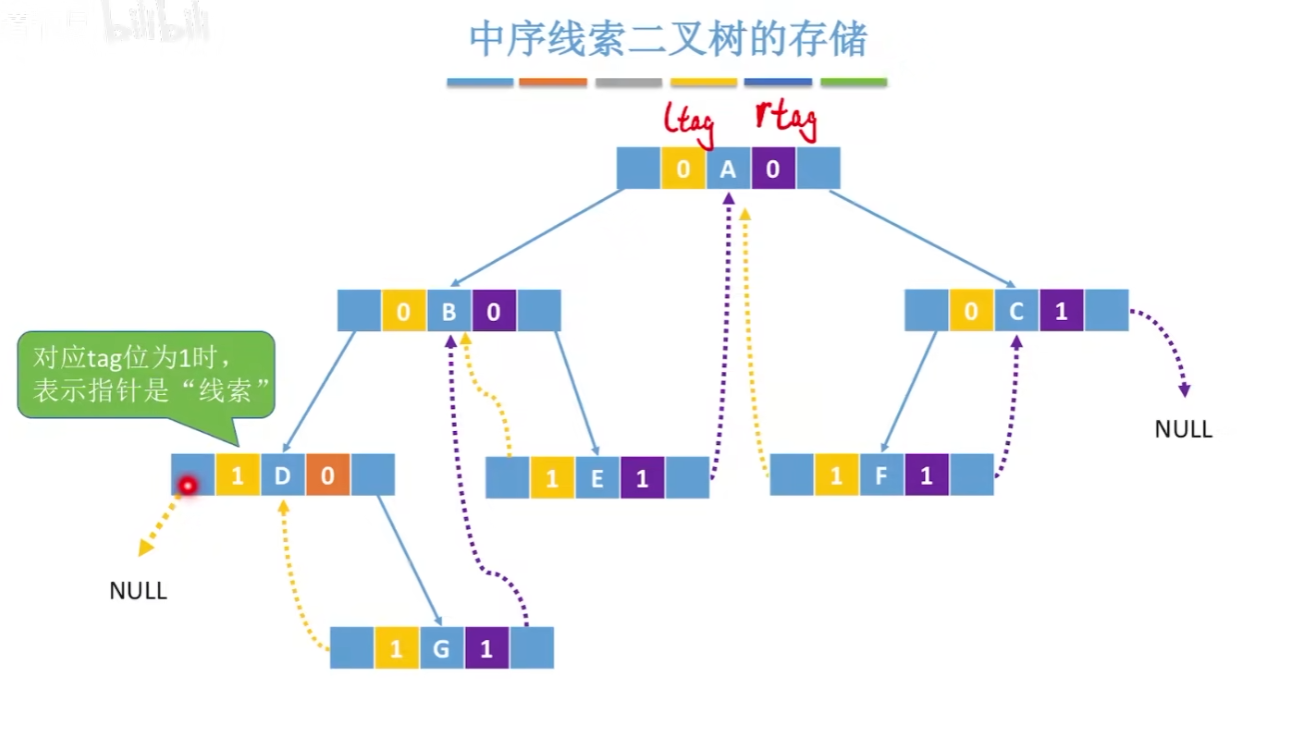
12-7、二叉树线索化,对visit函数进行实现
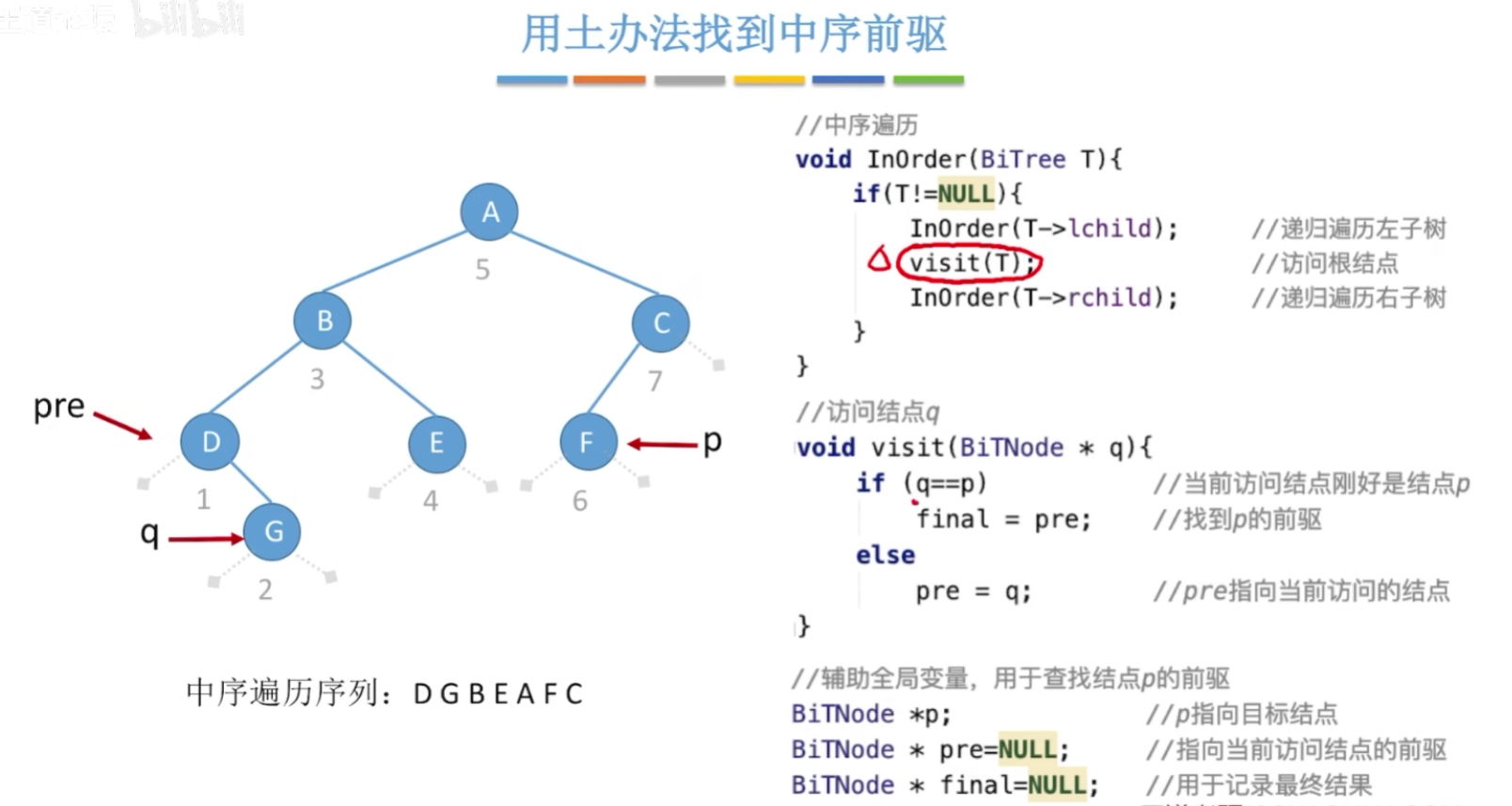
线索化先要对二叉树进行一次完整遍历。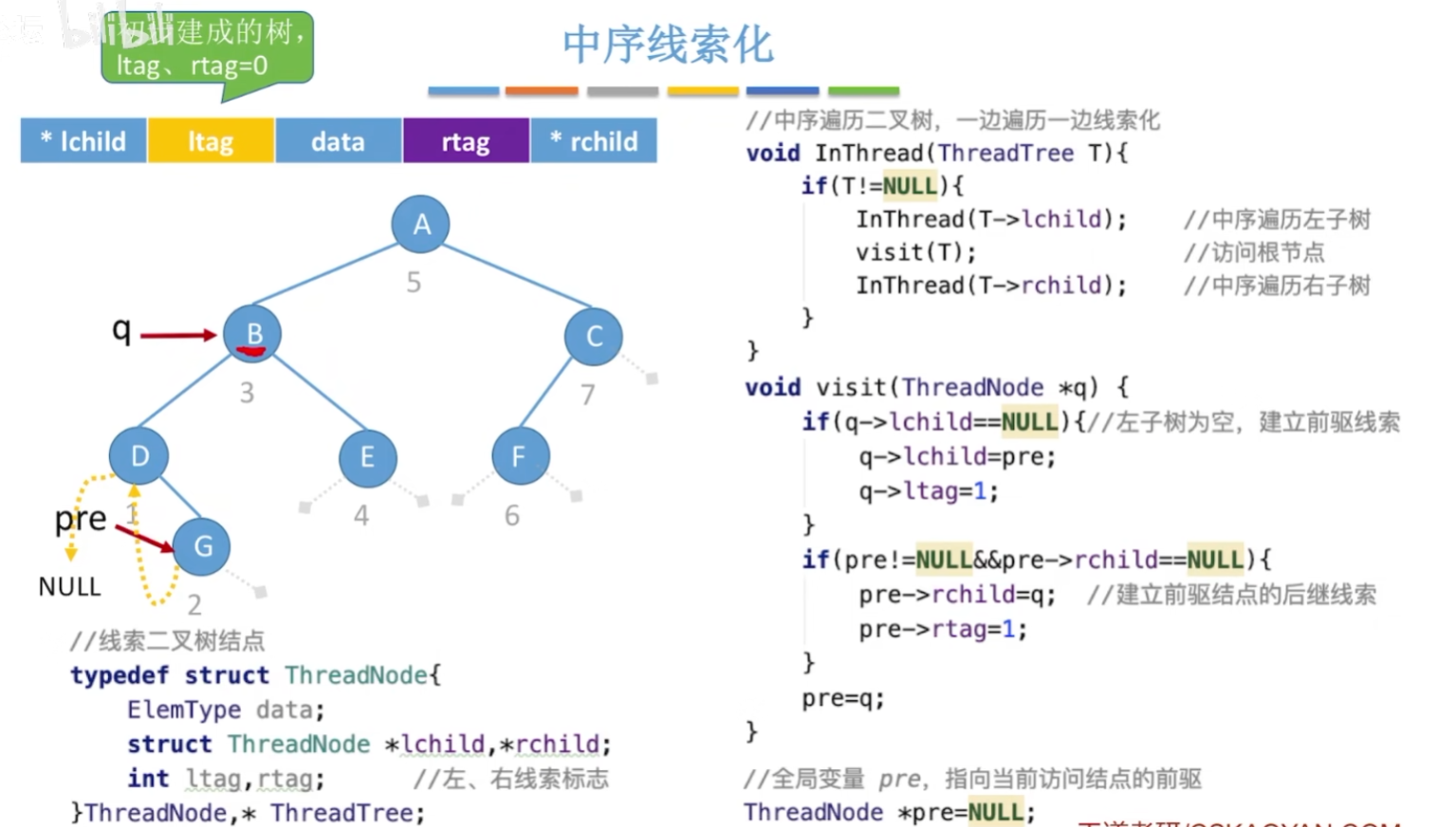
中序线索化完整代码如下:

先序线索化代码:
后续线索化代码:
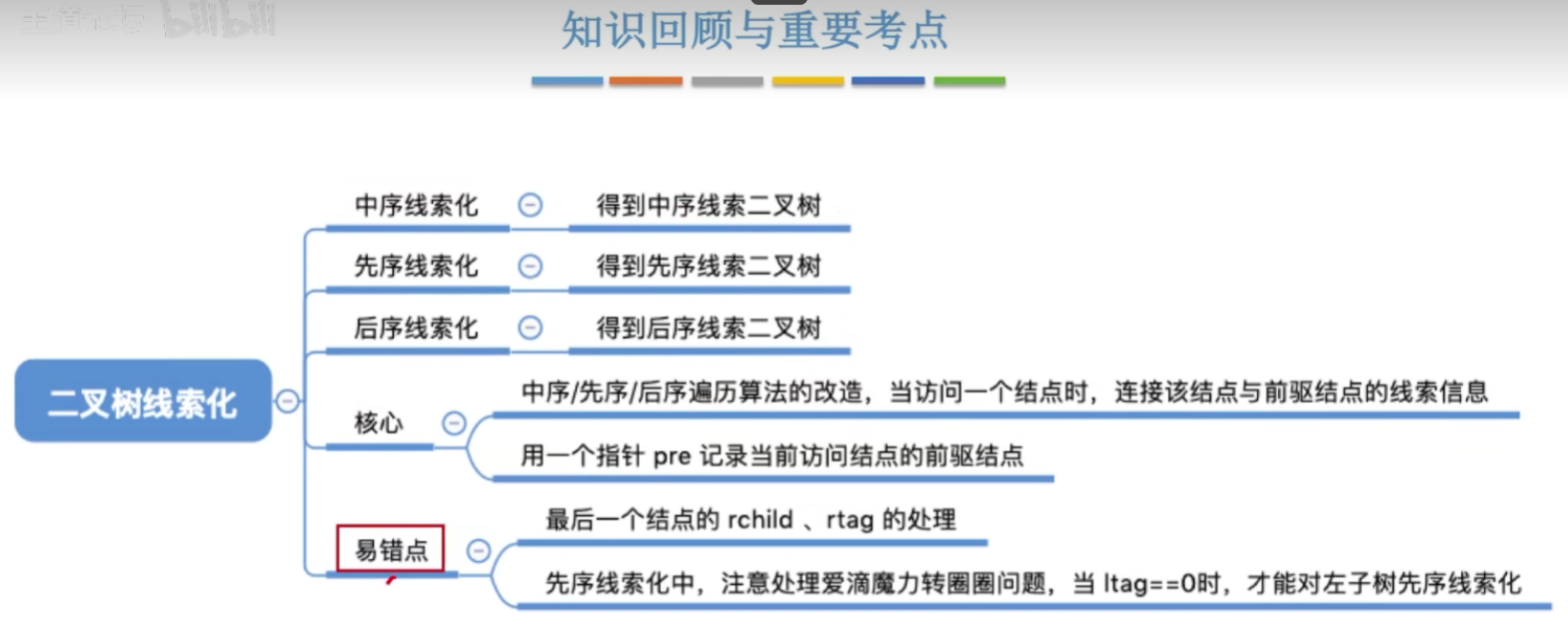
12-8、二叉树中序找后继和前驱
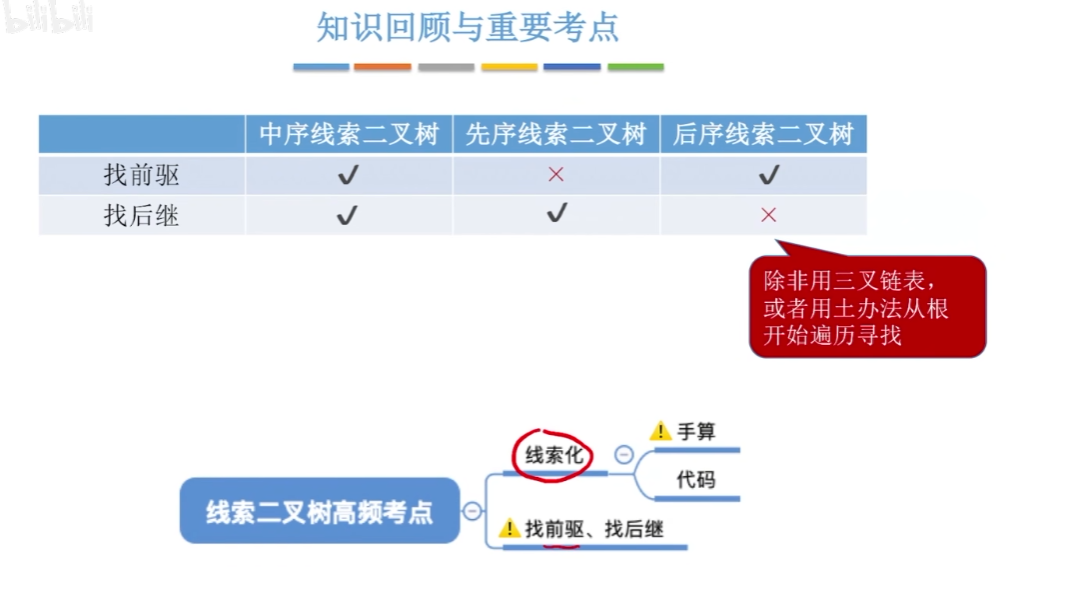

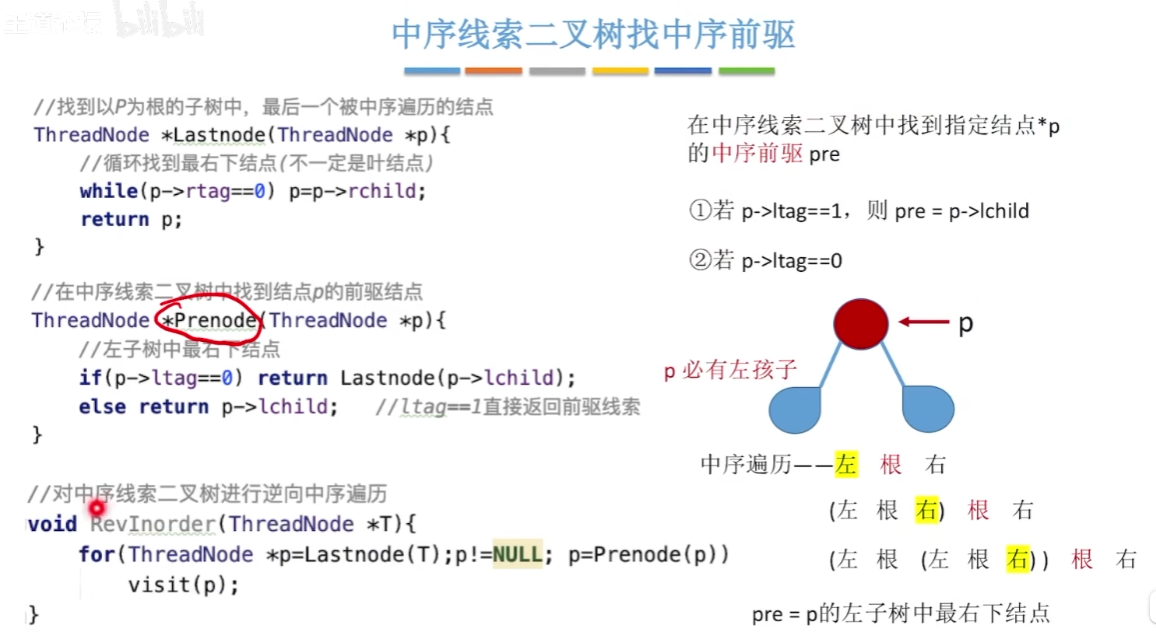
12-9、树的存储
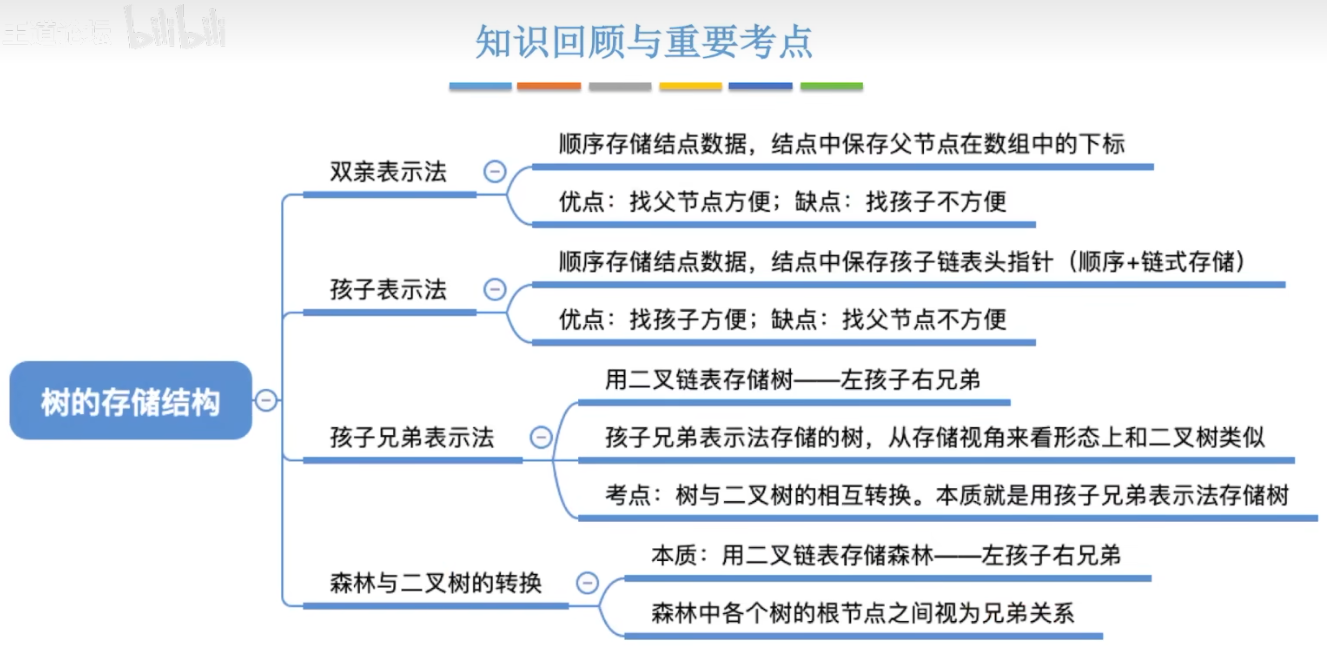
二叉树的顺序存储,使用数组存储,至于链式存储在上面已经讲过了。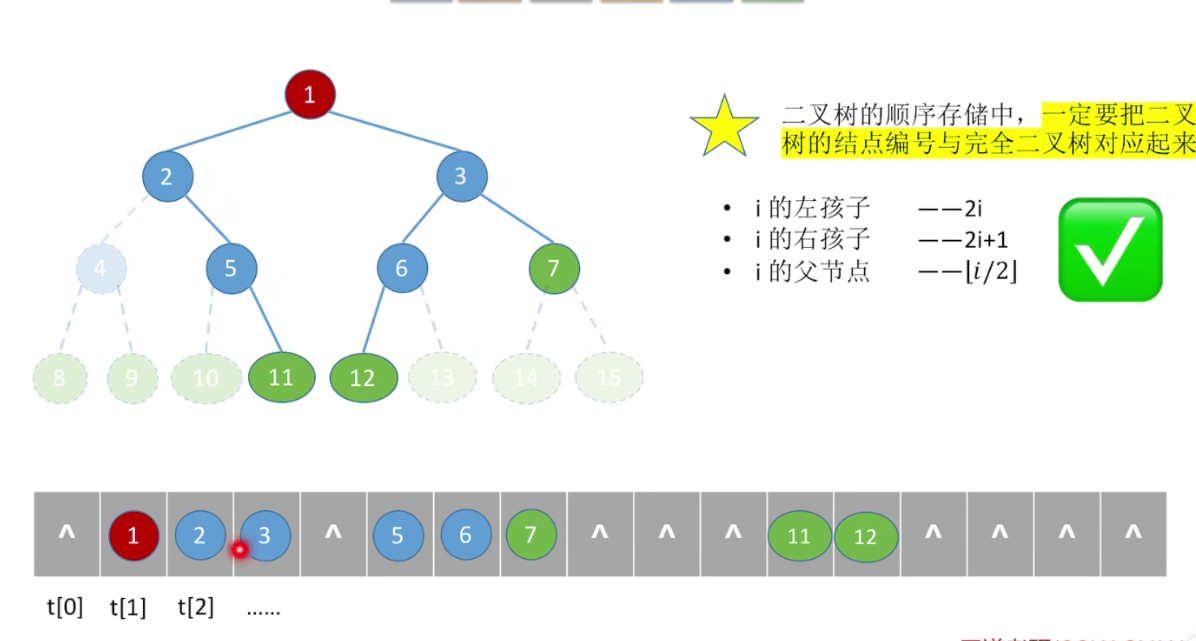
其他树: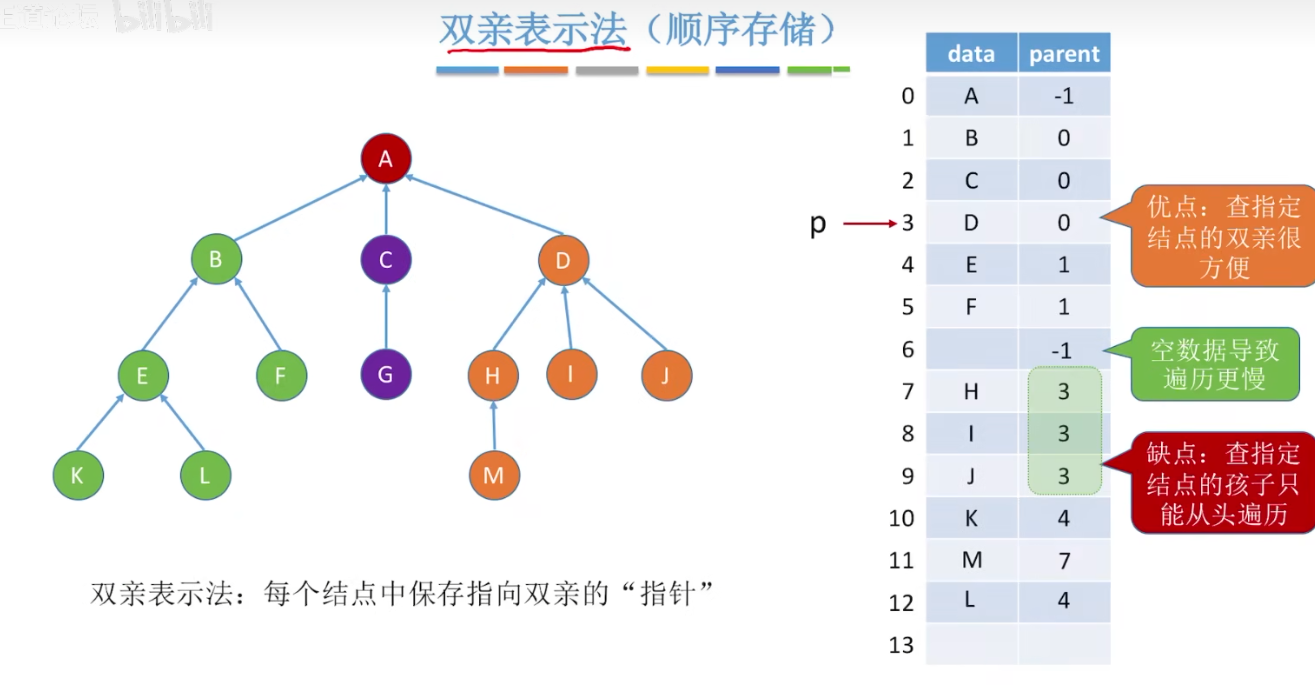
二叉树也可以以用这个方法存储。
孩子表示法:顺序+链式存储: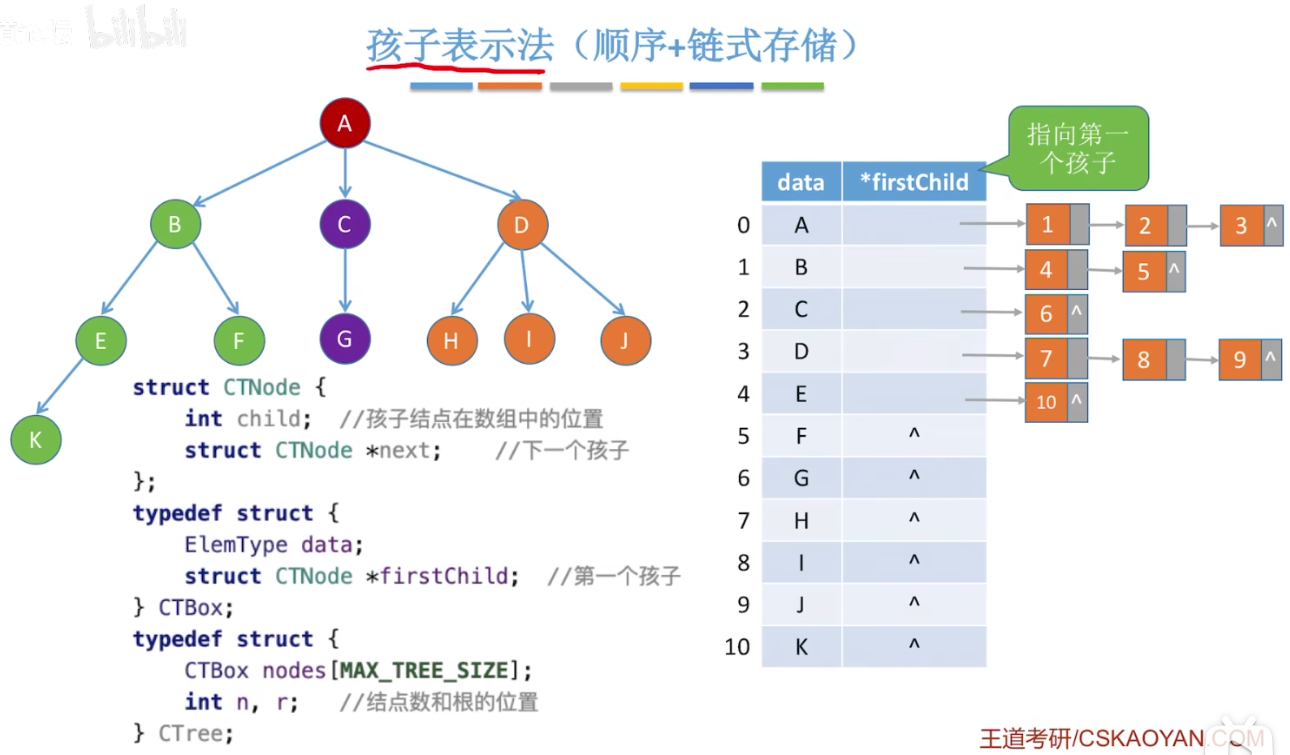
兄弟孩子表示法:链式存储:
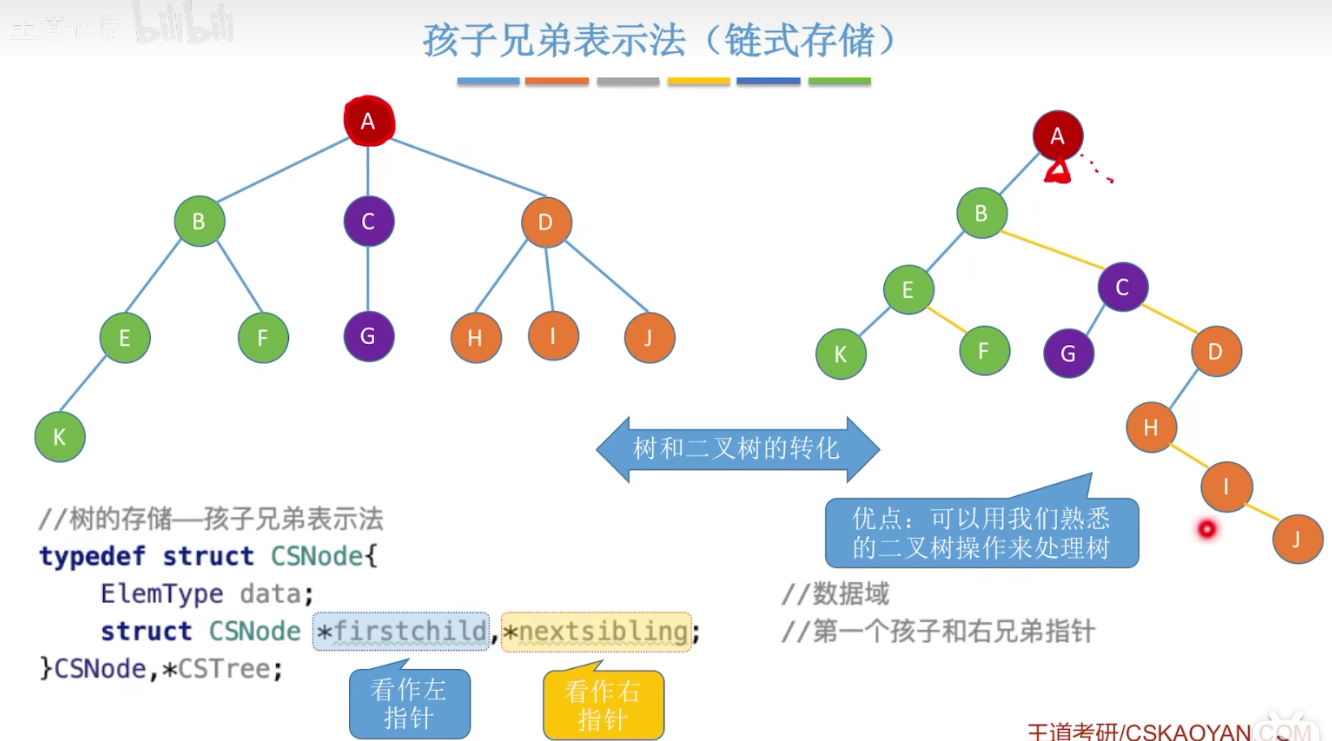
树和二叉树的转化:
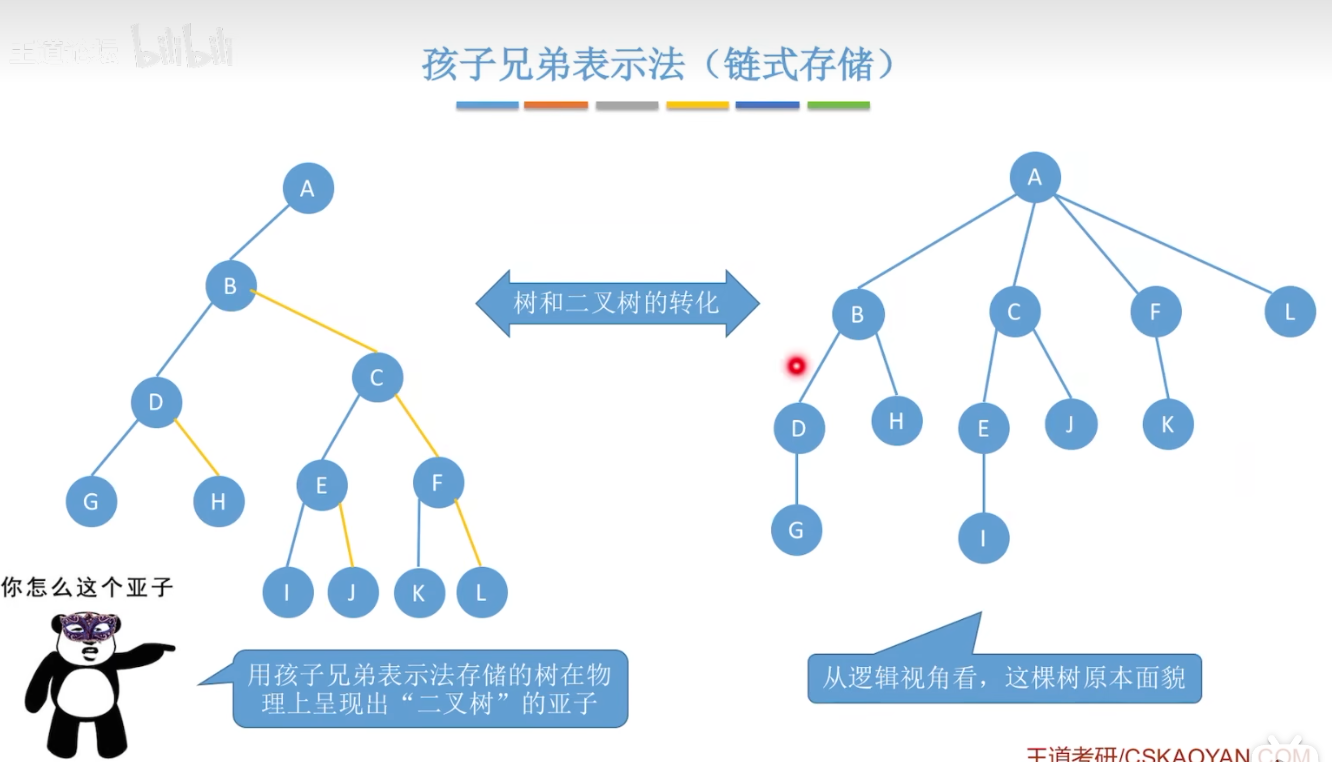
森林转化成二叉树:
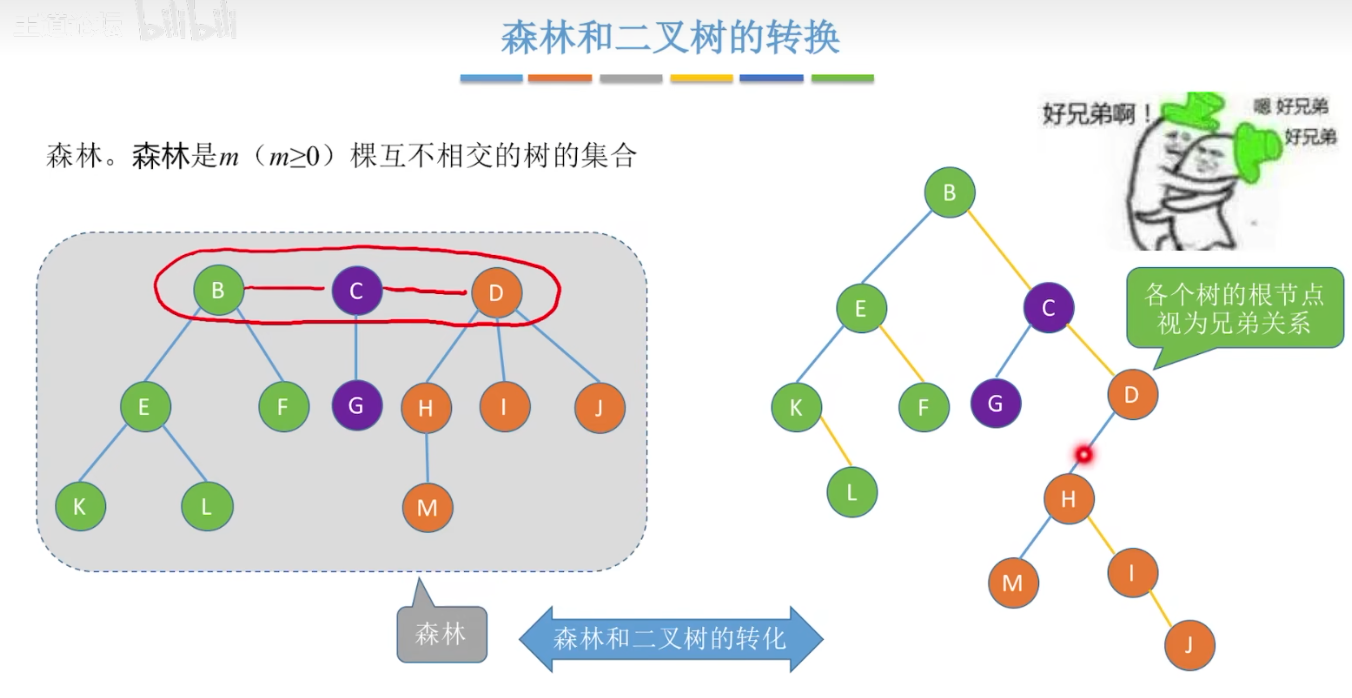
12-10、树的遍历
树的先根遍历,实现后达到树和二叉树的转化: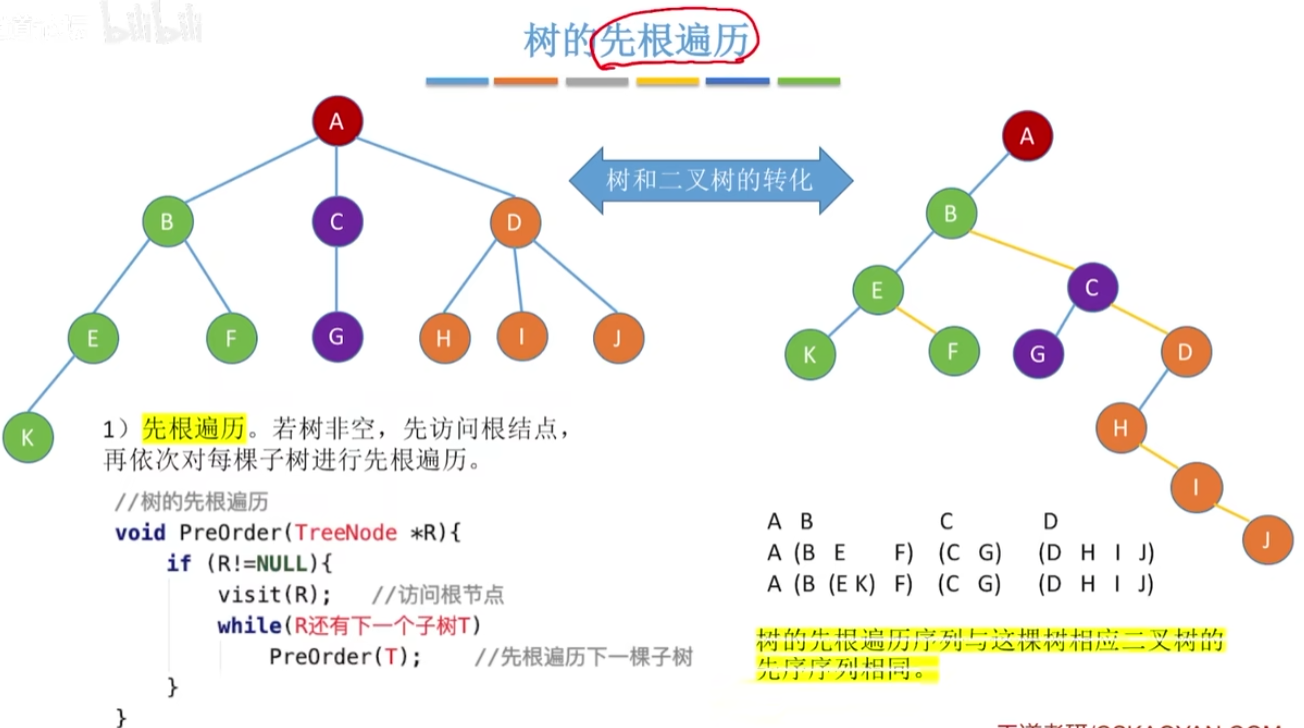
树的后续遍历,实现二叉树和树的转化:
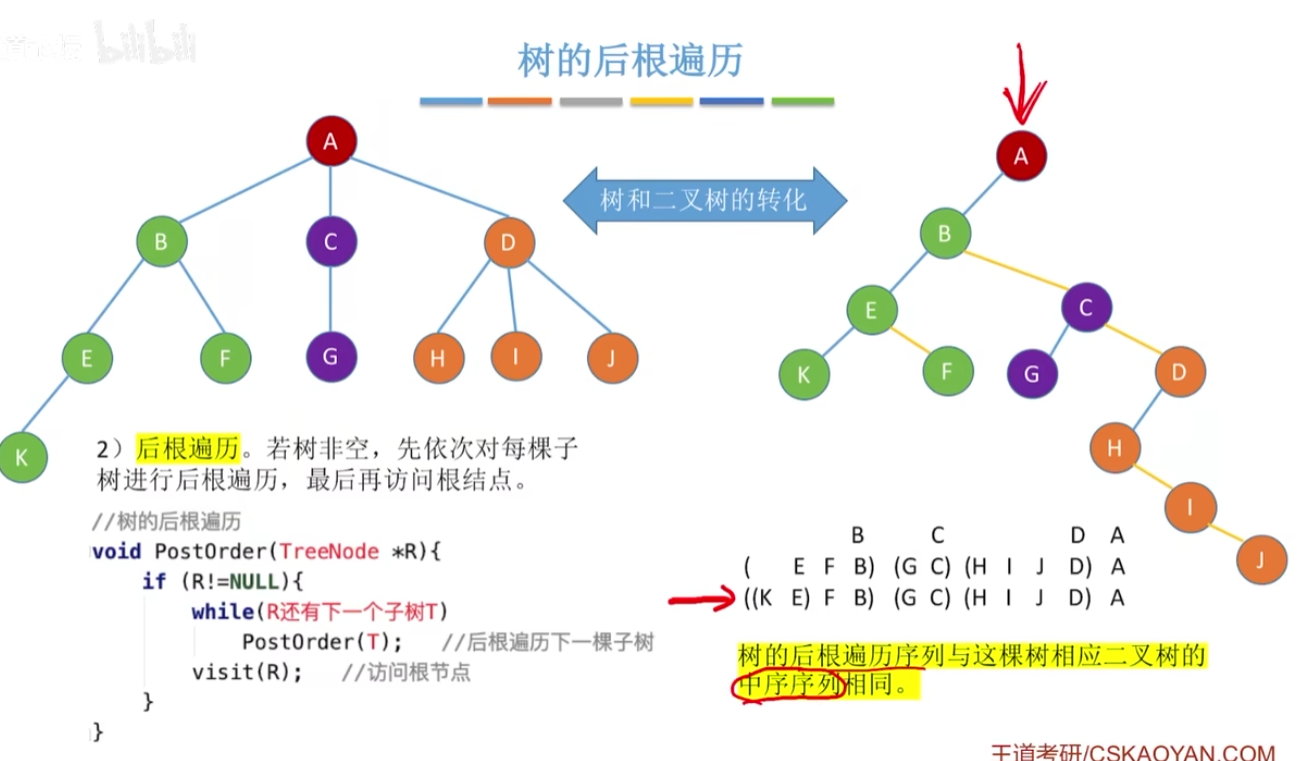
树的层序遍历: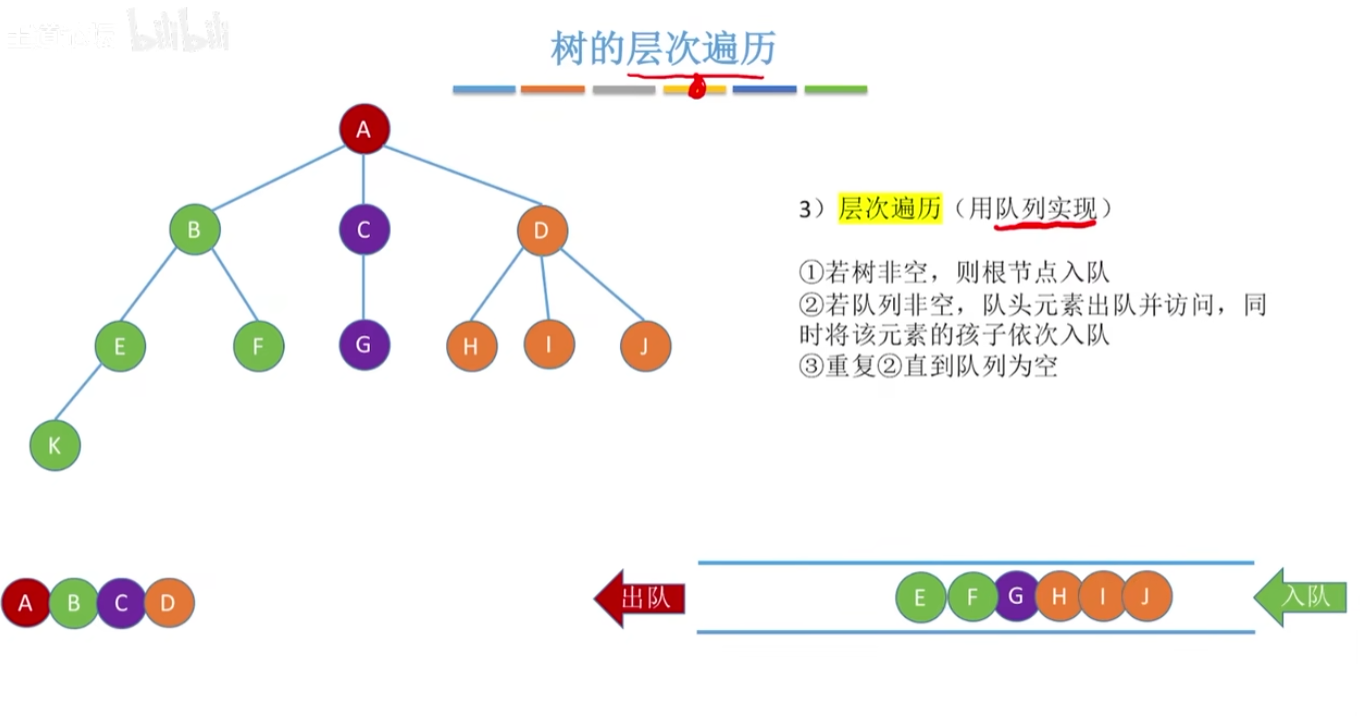
12-11、哈夫曼树
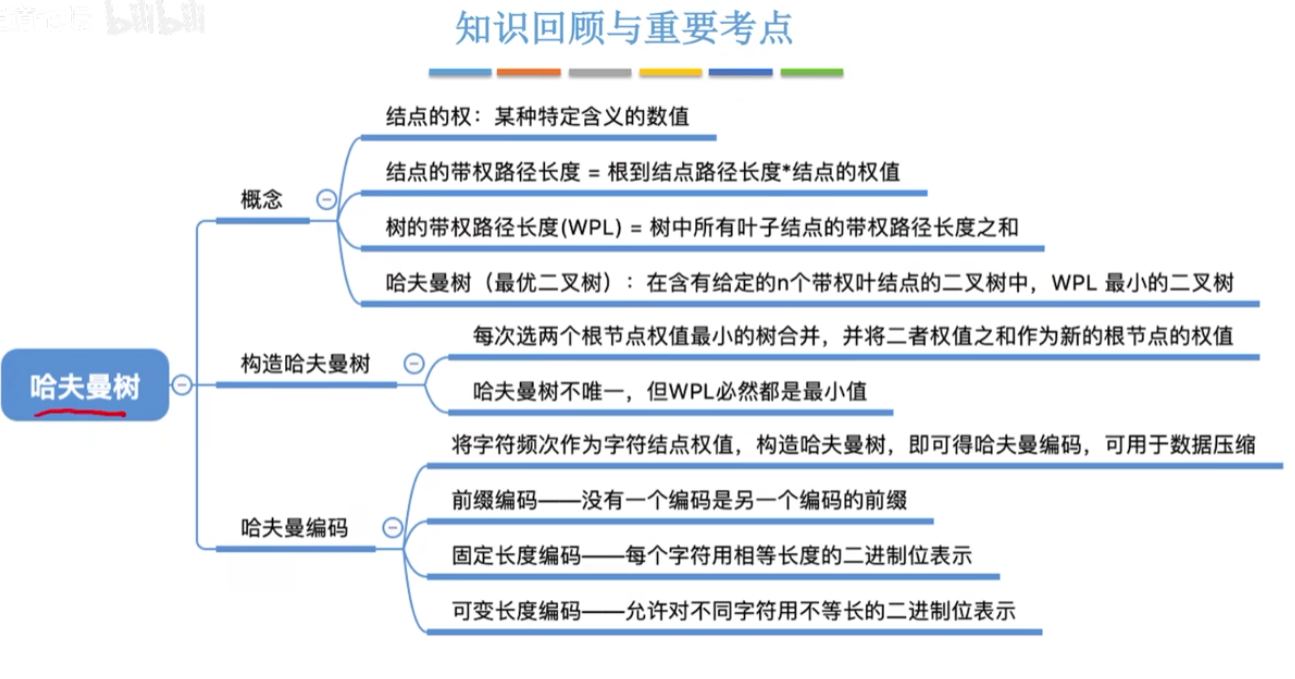
节点的权:节点上数据所表示的某种信息量。
节点的带权路径长度:从根节点到该节点的路径长度与该节点上数据的乘积。
哈夫曼树:带权路径长度最小的二叉树。也称为最优二叉树。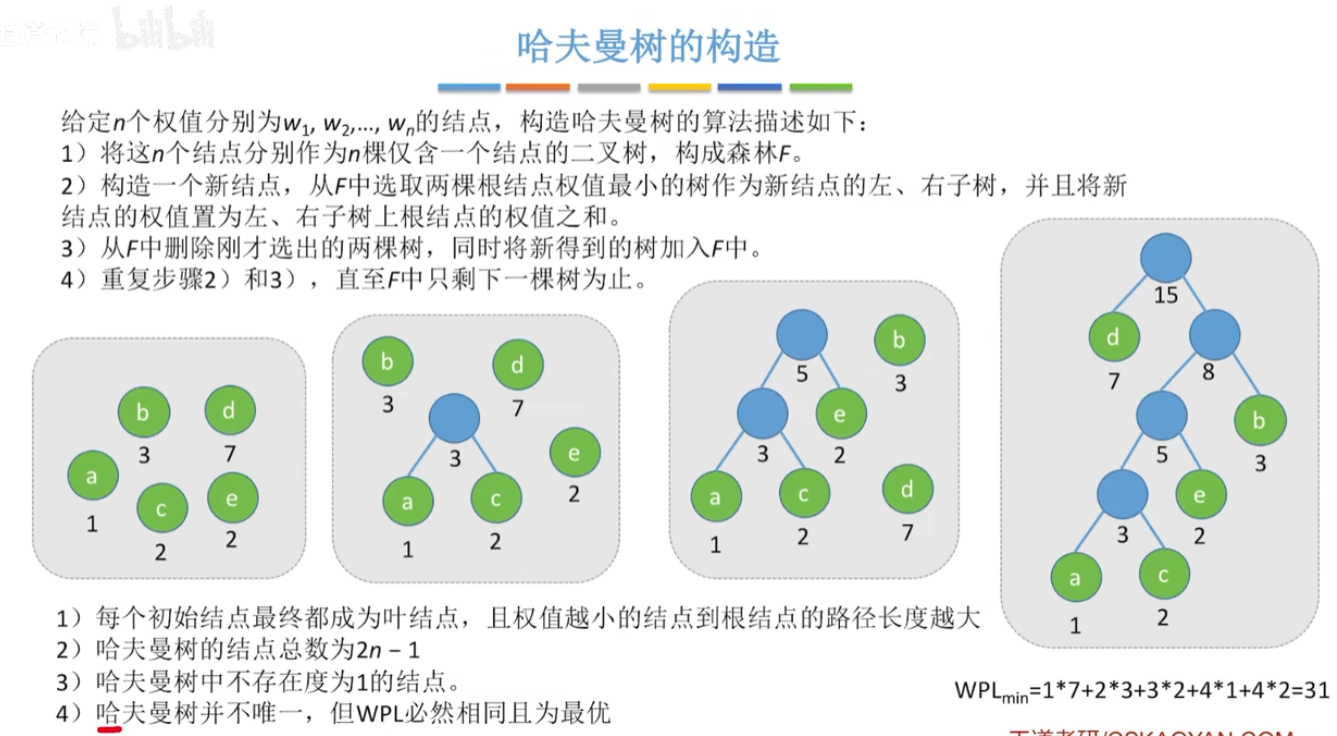
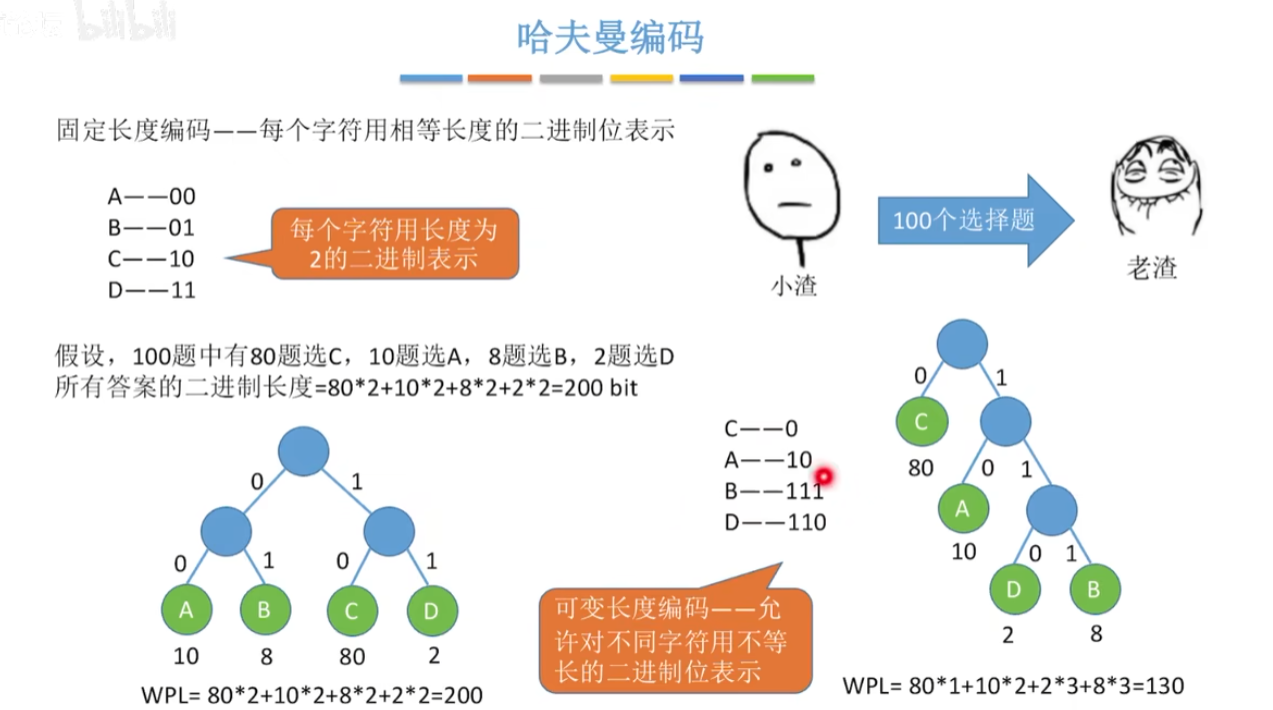
应用:哈夫曼编码。(可变长度编码)
一般的ascii码是定长编码,一个字节8位。
哈夫曼编码:将字符按照出现频率从高到低排序,然后两两合并,合并后字符频率和合并前字符频率之和就是合并后字符频率。