计算机组成原理
1、计算机发展
计算机系统 = 硬件 + 软件
软件分为:
系统软件: 用来管理整个计算机系统的软件(操作系统、标准程序库、数据库管理系统、网络软件(如tcp/ip)、语言处理程序、服务程序(如:调试程序)等)
应用软件: 按任务需要编制的各种程序
早期的计算机是使用手动接线来控制的计算,冯·诺依曼提出了 “存储程序”的概念,即指令以二进制代码的形式事先输入计算机的主存储器中,计算机执行指令的过程就是从主存储器中取出指令并执行的过程。
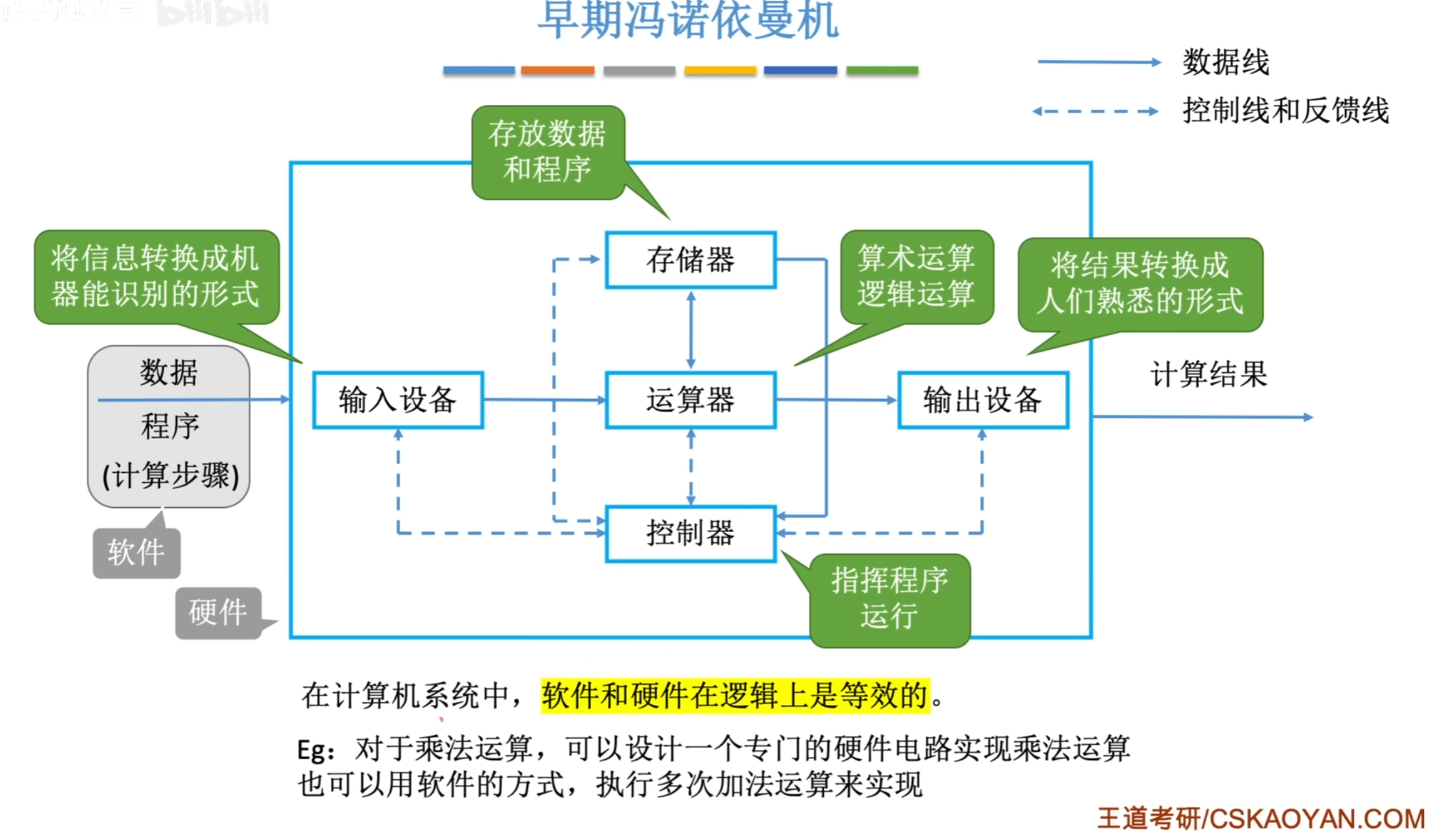
冯·诺依曼计算机的结构特点
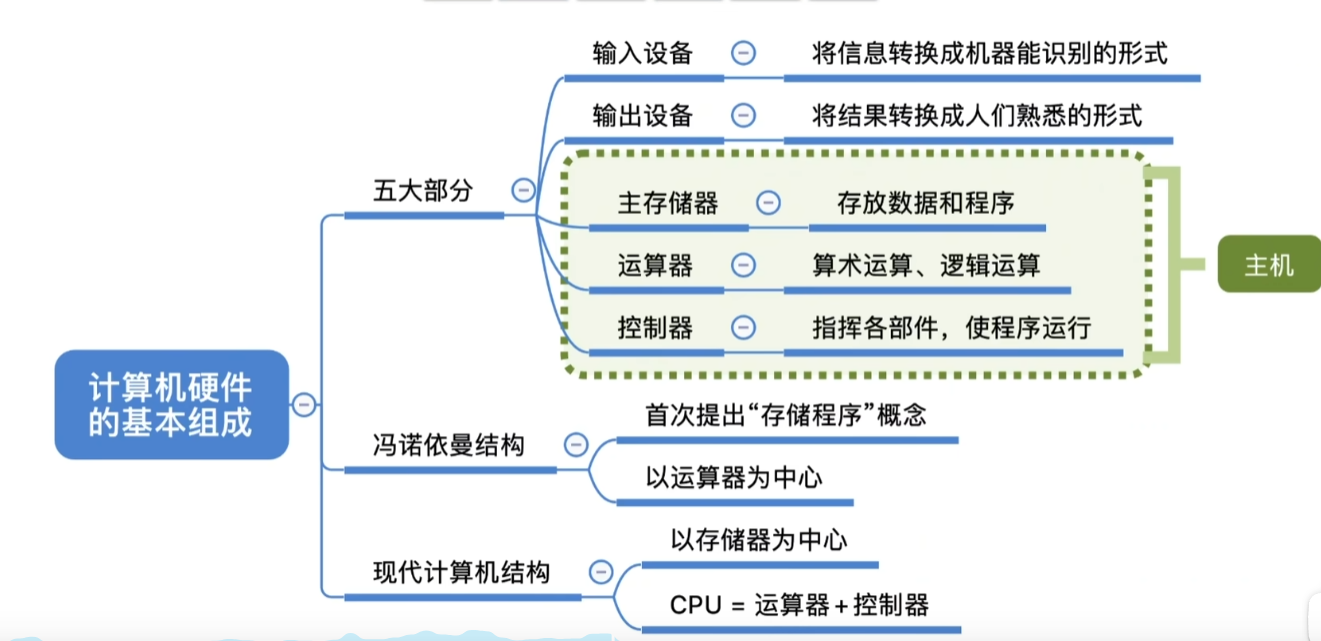
1、计算机由五大部件组成。
2、指令和数据以同等地位存于主存储器中,可按地址寻址。
3、指令和数据用二进制表示。
4、指令由操作码和地址码组成。
5、存储程序。
6、以运算器为中心。(输入/输出设备与存储器之间的数据通过运算器进行传输)
上面经过优化,将存储器放到中心,得到现代的计算机结构。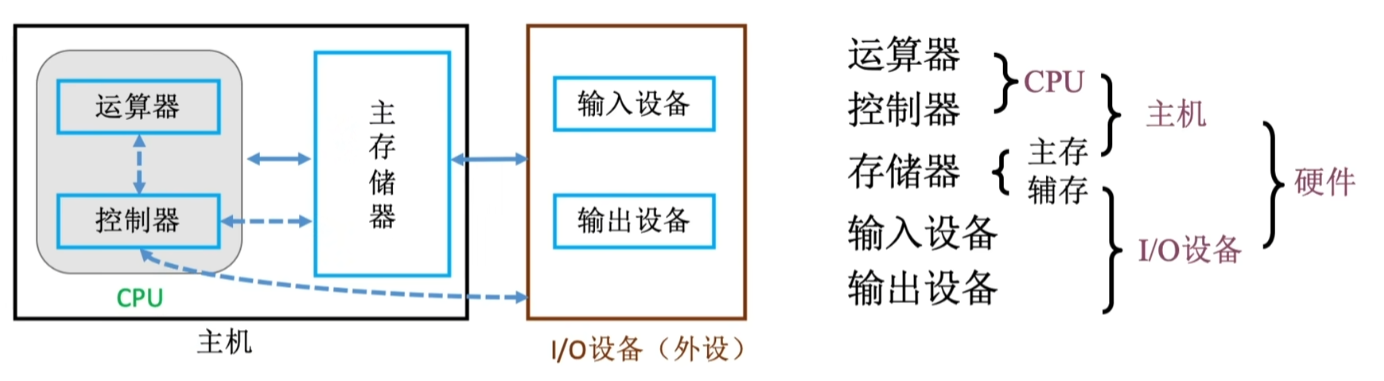
2、各个硬件的工作原理
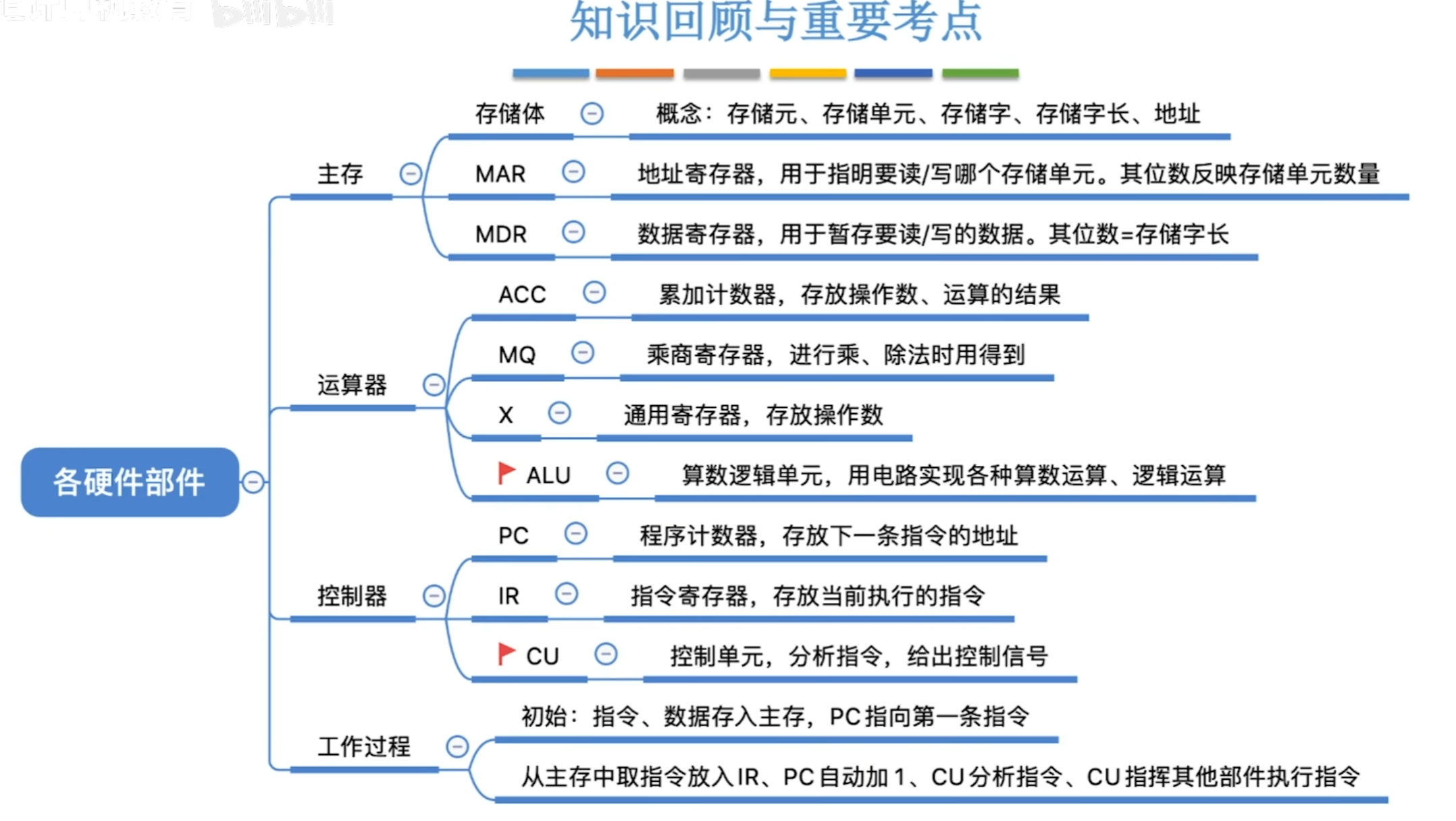
计算机中,cpu内部由主存储器,控制器,运算器构成
- 主存储器:由存储体,MAR(Memory Address Register)(存储地址寄存器)和MDR(Memory Data Register)(存储数据寄存器)组成。
cpu对MAR进行寻址,将数据存入MDR中,或者读出数据。
存储单元:每个存储单元存放一串二进制代码。
存储字:存储单元的容量,一般为8位或16位。
存储字长:存储单元中二进制代码的位数。
存储元:存储二进制的电子元件,每个存储元为1bit。
MAR:通过位数可以知道存储单元的个数,通过地址线可以知道每个存储元的编号。
MDR:通过位数可以知道储存单元的储存字长。

易混淆:
1个字节(1byte)=8位(bit)
1B=1个字节,1b=8b
运算器:用于实现算数运算(如加减乘除),逻辑运算(与或非)。由ACC(累加器,用于存放操作数,或者运算结果)、MQ(乘商寄存器,在乘、除运算时,用于存放操作数或运算结果)、X(通用的操作数寄存器,用于存放操作数)、ALU(算数逻辑单元,通过内部复杂的电路实现算数运算、逻辑运算)。
ACC、MQ、X这三个主要是用来存放运算结果或数值的,ALU是用来实现算数运算和逻辑运算的。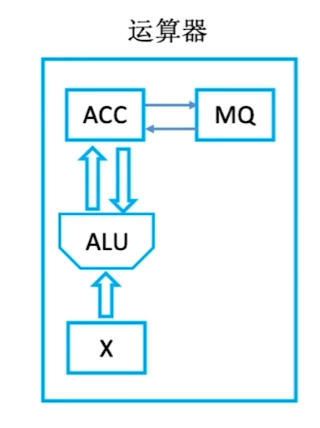
控制器:由CU(控制单元,分析指令,给出控制信号)、IR(指令寄存器,存放当前的执行指令)、PC(程序计数器,存放下一条指令的地址,有自动加1功能)
完成一条指令:PC取指令,放到IR中分析指令,CU分析指令,给出控制信号。
- 举例将上述的程序编译成二进制代码,存入主存储器中。
1
2
3
4
5
6int a = 10; b = 20; c = 2;
int main()
{
int d = a*b+c
return 0 ;
}
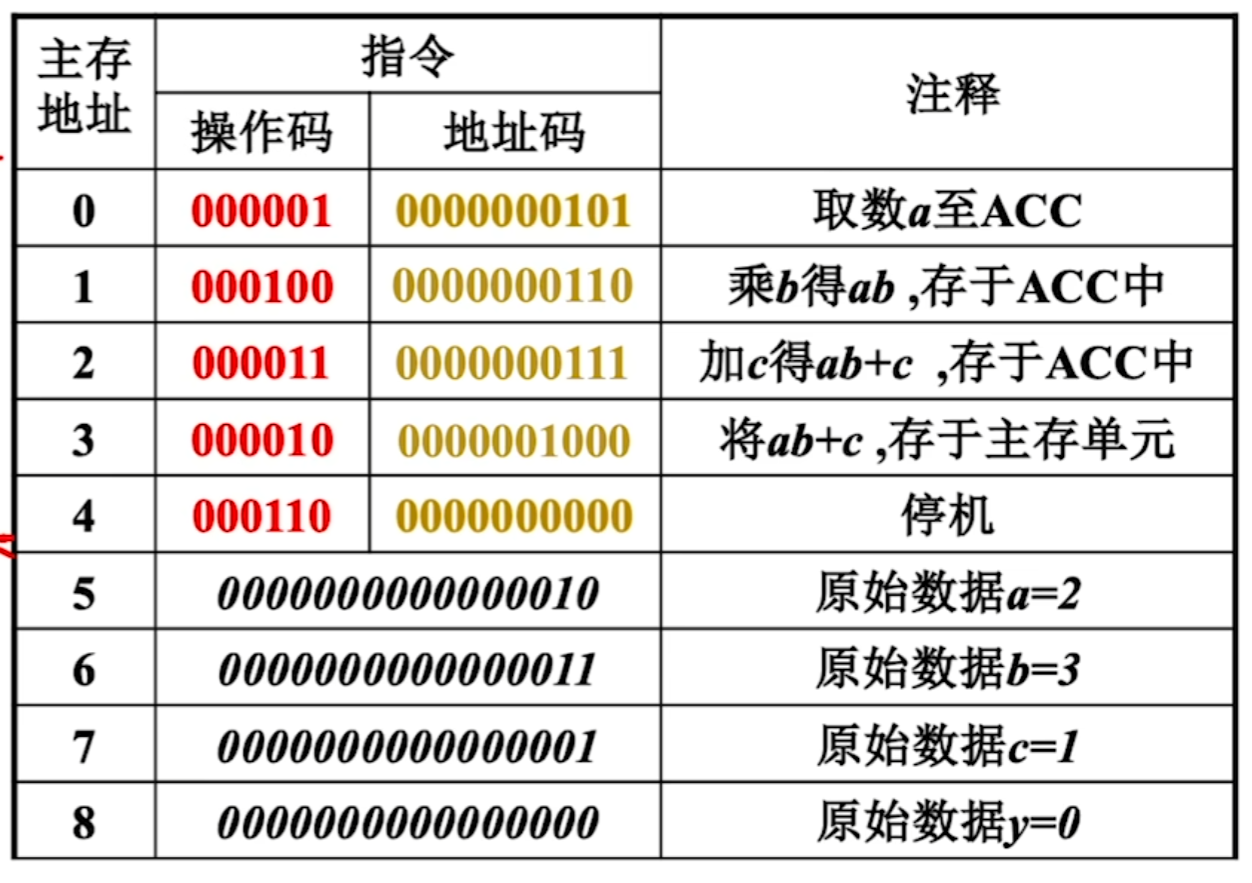
下面是cpu运行的过程
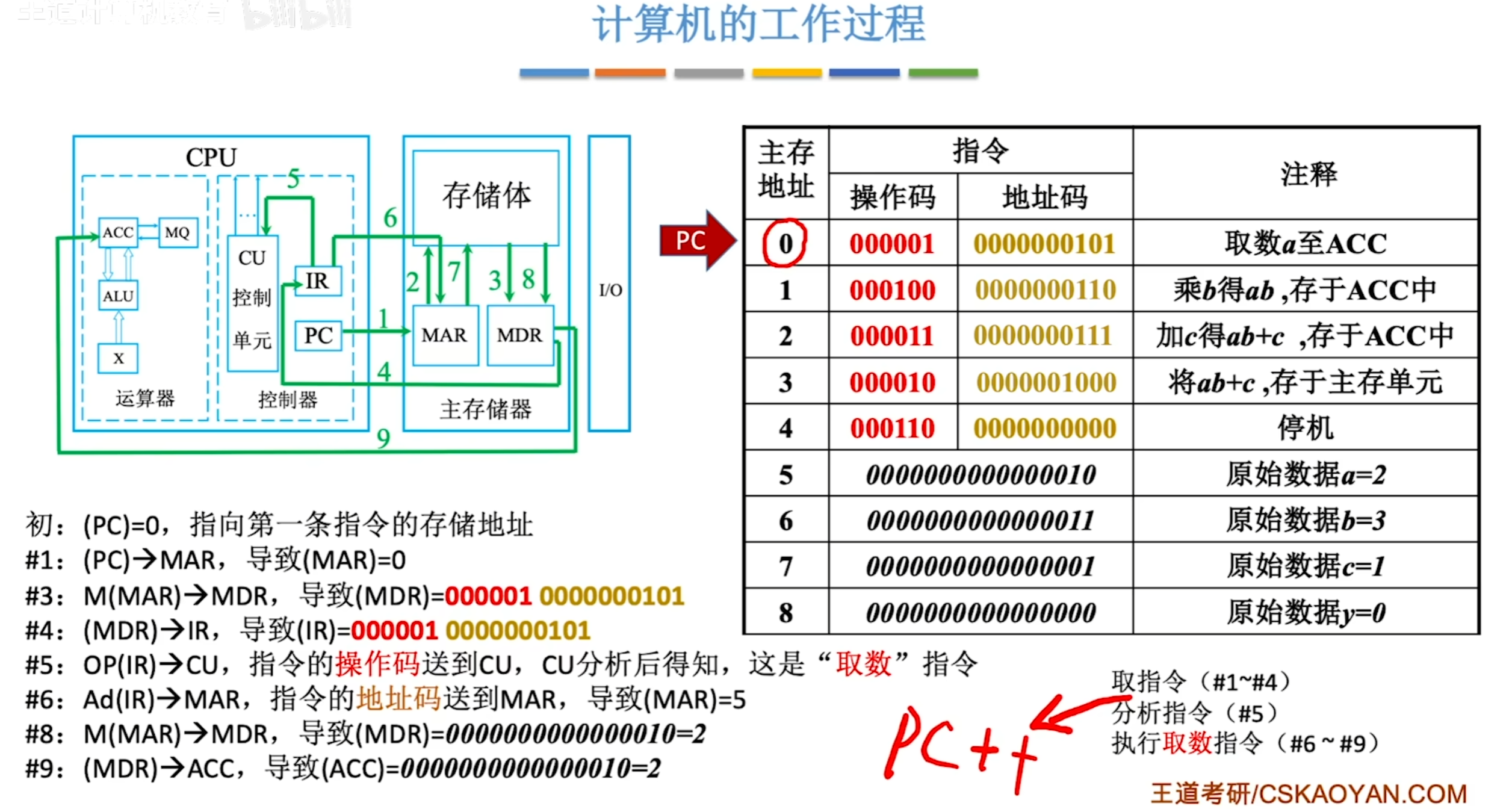
上图中,这是执行主存地址0号地址的步骤,执行完0号地址的步骤后,PC自动加1,指向1号地址重复。
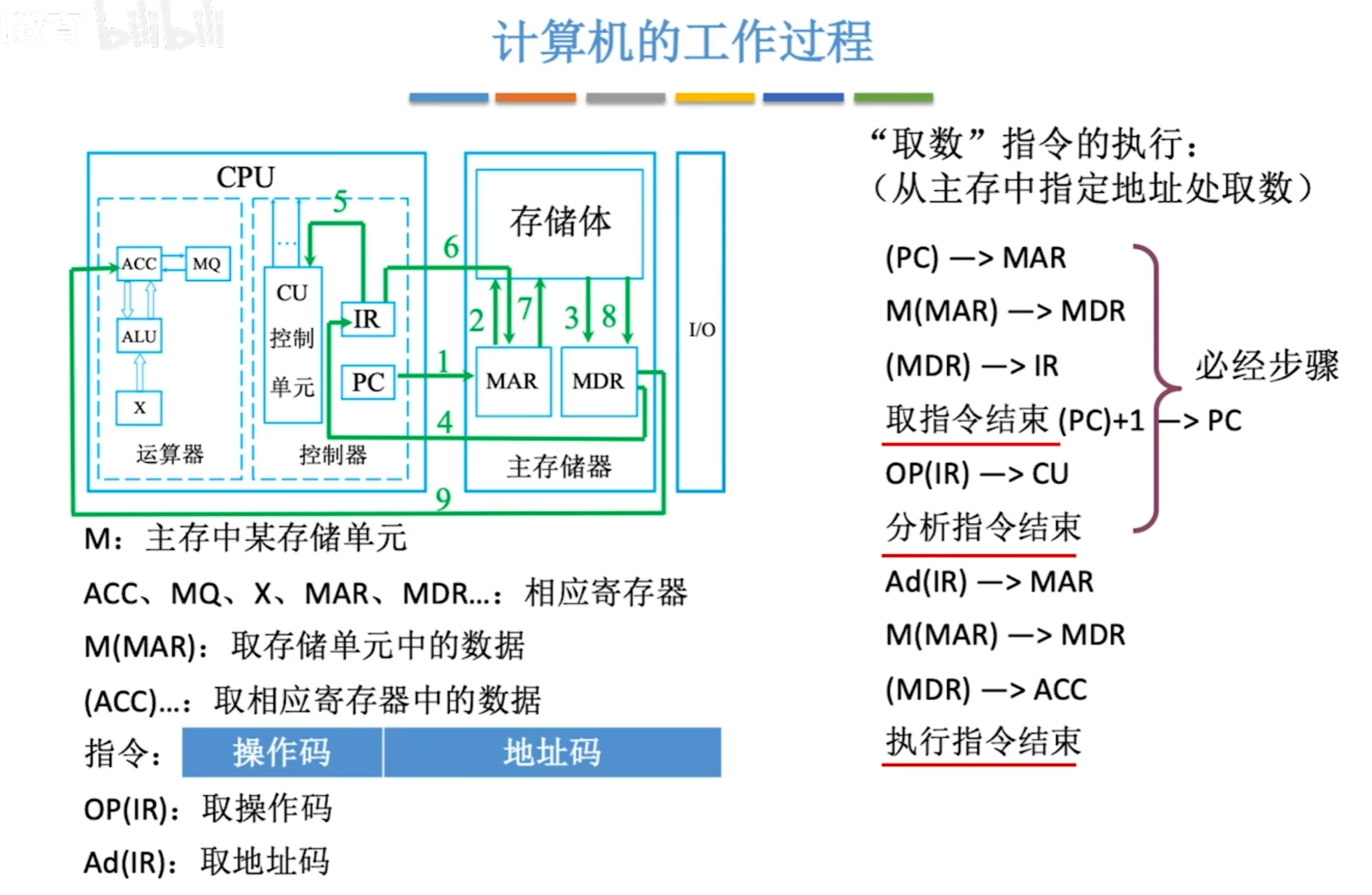
cpu区分指令和数据的依据:指令周期的不同阶段。
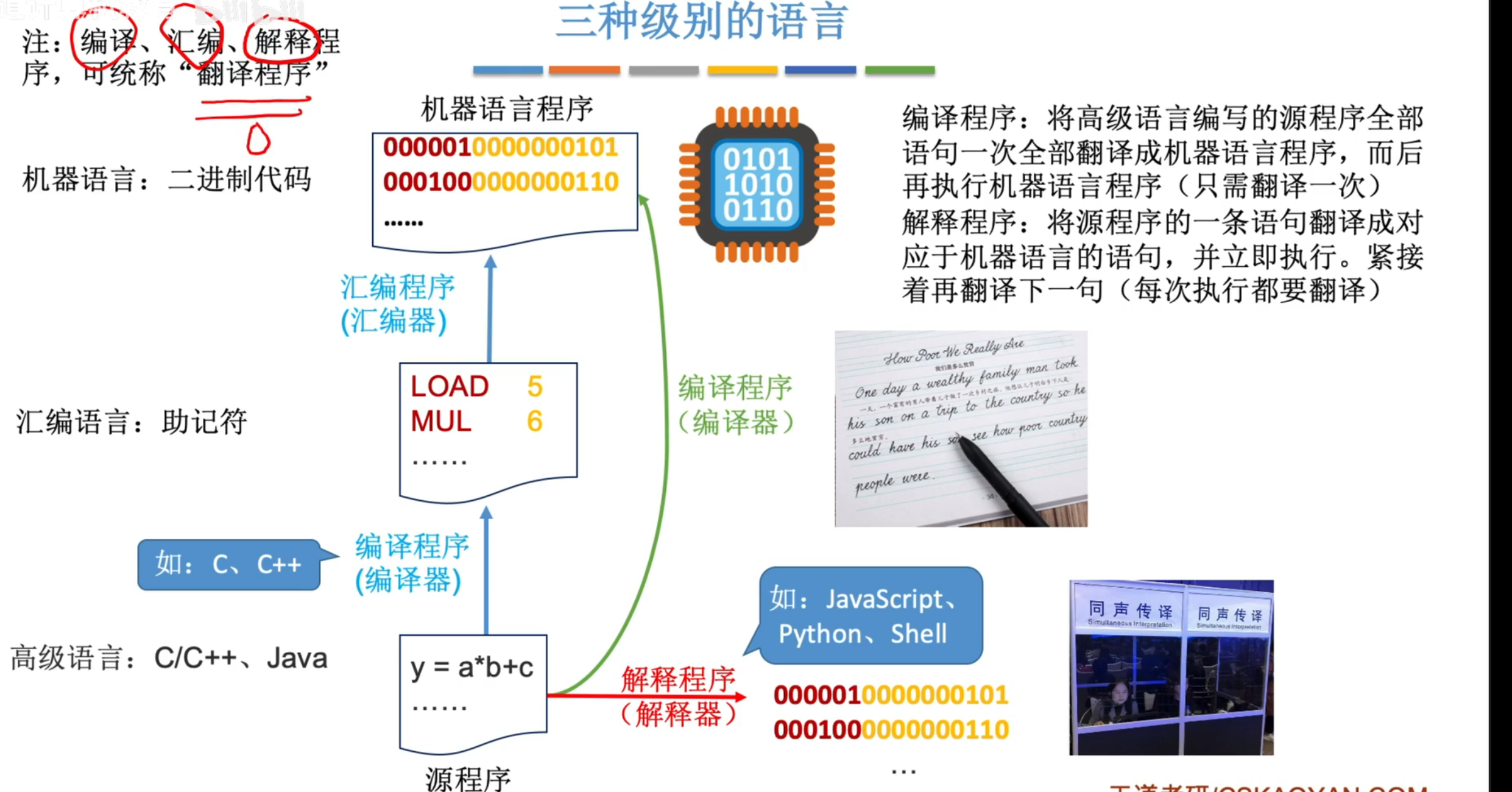
3、计算机系统的层次结构

4、计算机的性能指标
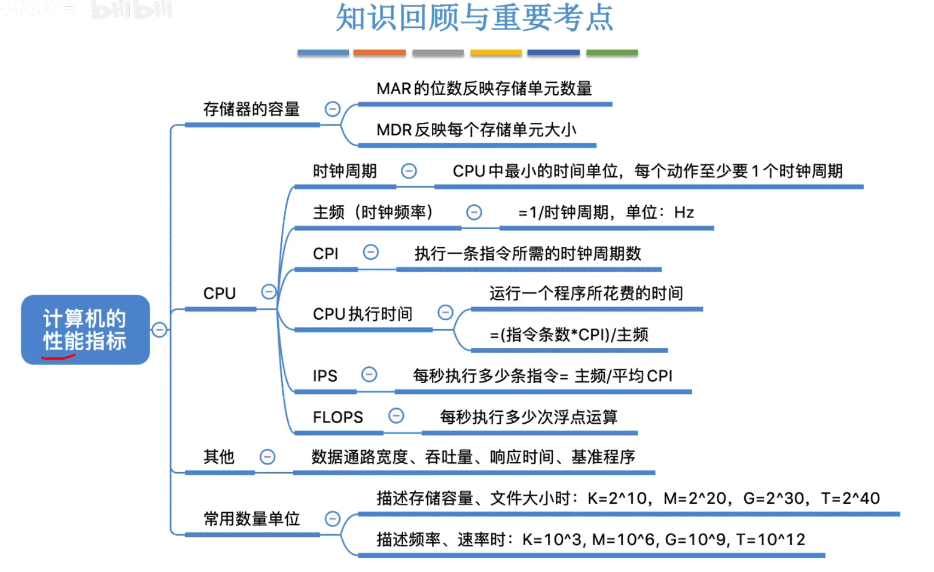
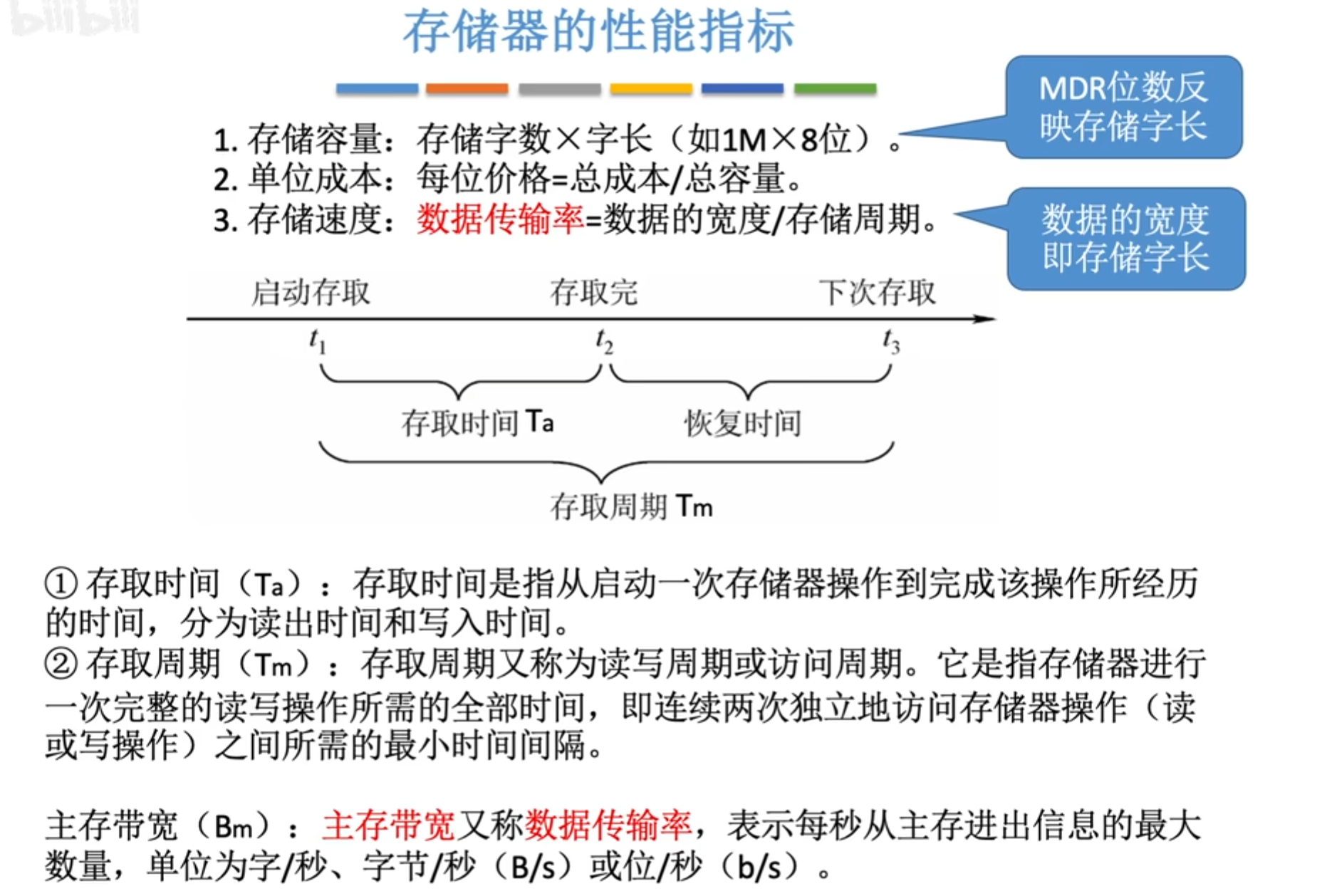
4.1、存储器的性能指标
主存储器中,MAR的位数可以得到存储单元的位数。MDR的位数可以得到存储单元的容量。
总容量 = 存储单元的个数 * 存储字节长 bit = 存储单元个数X存储字长/8 Byte
例如MAR = 32位 。MDR = 8位
总容量 = 2^32 * 8 = 4GB
2^10 = k; 2^20 = M; 2^30 = G ; 2^40 = T
4-2、CPU的性能指标
cpu主频:cpu工作的时钟频率。
cpu时钟周期:cpu工作一次的时间。主频的倒数。
CPI:指令周期数。(不同的指令,执行时间不同,甚至是相同的指令,执行时间也可能不同,或者如果负荷比较大,执行时间也可能不同)
执行一条指令的时间 =CPI * cpu时钟周期
IPS:每秒执行多少指令。IPS=主频/CPI
FLOPD:每秒执行多少条浮点指令。
4-3、系统的整体性能指标
数据通路带宽:数据总线一次所能并行传送的信息的位数
吞吐量:单位时间内处理请求的数量
响应时间:从发出请求到收到响应的时间
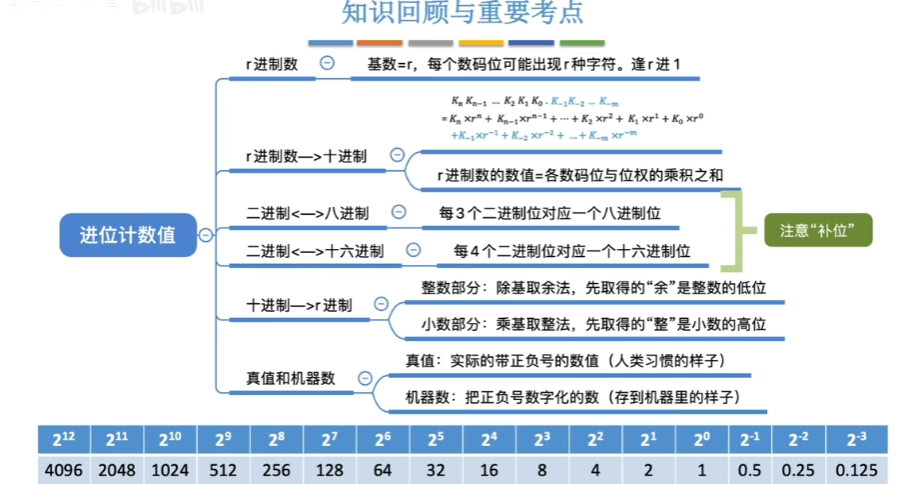
5、进位计数制
比较简单,略过。
10进制小数化为二进制小数
如:0.3
- 0.3 * 2 = 0.6 = 0 + 0.6
- 0.6 * 2 = 1.2 = 1 + 0.2
- 0.2 * 2 = 0.4 = 0 + 0.4
- 0.4 * 2 = 0.8 = 0 + 0.8
- 0.8 * 2 = 1.6 = 1 + 0.6
- 0.6 * 2 = 1.2 = 1 + 0.2
- 0.2 * 2 = 0.4 = 0 + 0.4
0.010010B
发现10进制小数无法化为二进制小数。只能无限循环下去。
2^-1 = 0.5
2^-2 = 0.25
5-1、BCD码
BCD码:二进制编码十进制数
主要有3类,8421码,余3码,2421码
8421码表示方法:比如985 = 1001 1000 0101
其他类似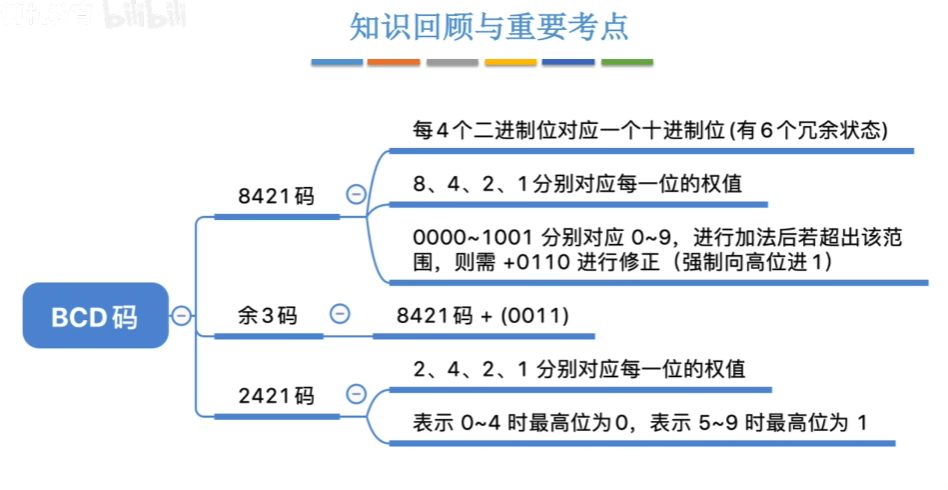
5-2、无符号数表示运算
机器字长决定了寄存器字长,决定了数据总线宽度。
无符号整数表示:假设机器字长为8,强行设置值为256,那么8为寄存器里值会都为0,有一个高位溢出了。
无符号整型减法则是:被减数不变,减数按位取反加1,得到减数补码。然后和被减数相加
5-3、有符号数表示运算
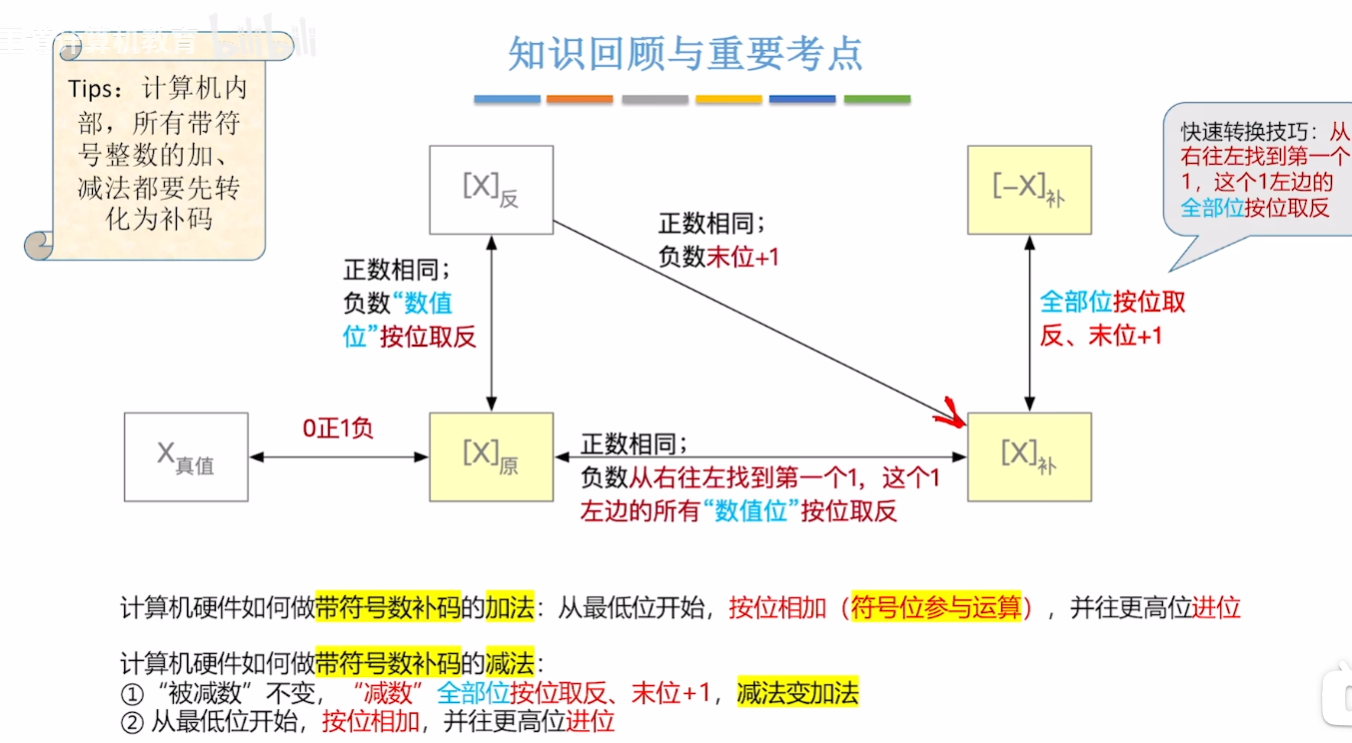
原码:最高位为符号位,0表示正数,1表示负数。真值0有两种特形式,-0和+0。
原码表示缺点:符号位和数值部分不能一起运算。需要设计复杂的电路
所以就需要反码和补码。反码目的是为了得到补码,补码是为了方便计算。
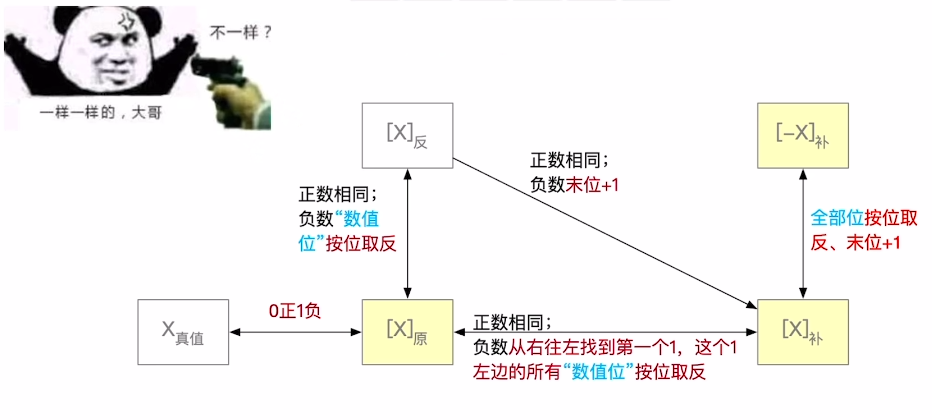
正数原码到补码:原码到反码不变,反码到补码也不变
负数原码到补码:原码到反码符号位不变,数值位取反,反码到补码末位加1,注意负数补码转反码不可逆。计算机处理的方式。
对于人类来说。可以省略反码,源码到补码的互相转变是:如果是负数,从右往左找到第一个1,这个1左边所有的数值位全部按位取反,如果是正数,补码和原码相同。
最后补码参与加法运算,符号位要参与运算。最后在转为原码。
如果是减法,则减数全部取反,包括符号位,末位加一。(计算机做法)
对于人类:从右往左找到第一个1,这个1左边所有的全部按位取反,包括符号位。
最终减法转换位加法操作。
5-4、移码
移码:符号位取反,数值部分不变。得到从0开始的数。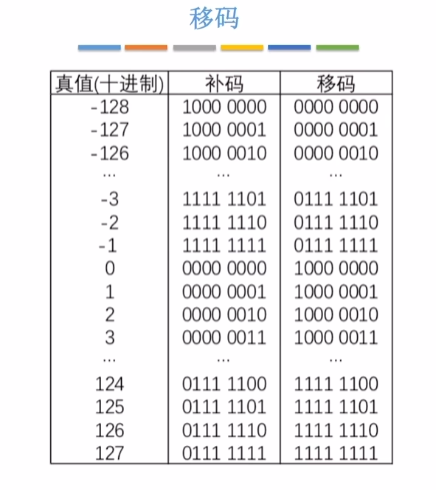
5-5、定点数
定点整数:编码表示有源码、反码、补码和移码四种表示方法。
定点小数:编码表示有原码、反码、补码三种。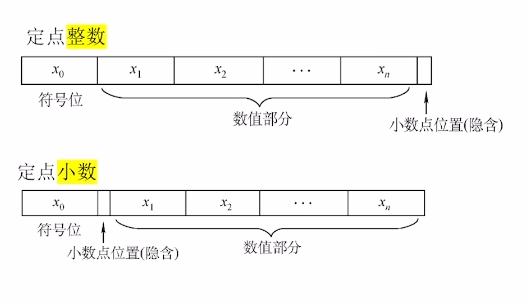
反码补码转换,和前面的内容一模一样
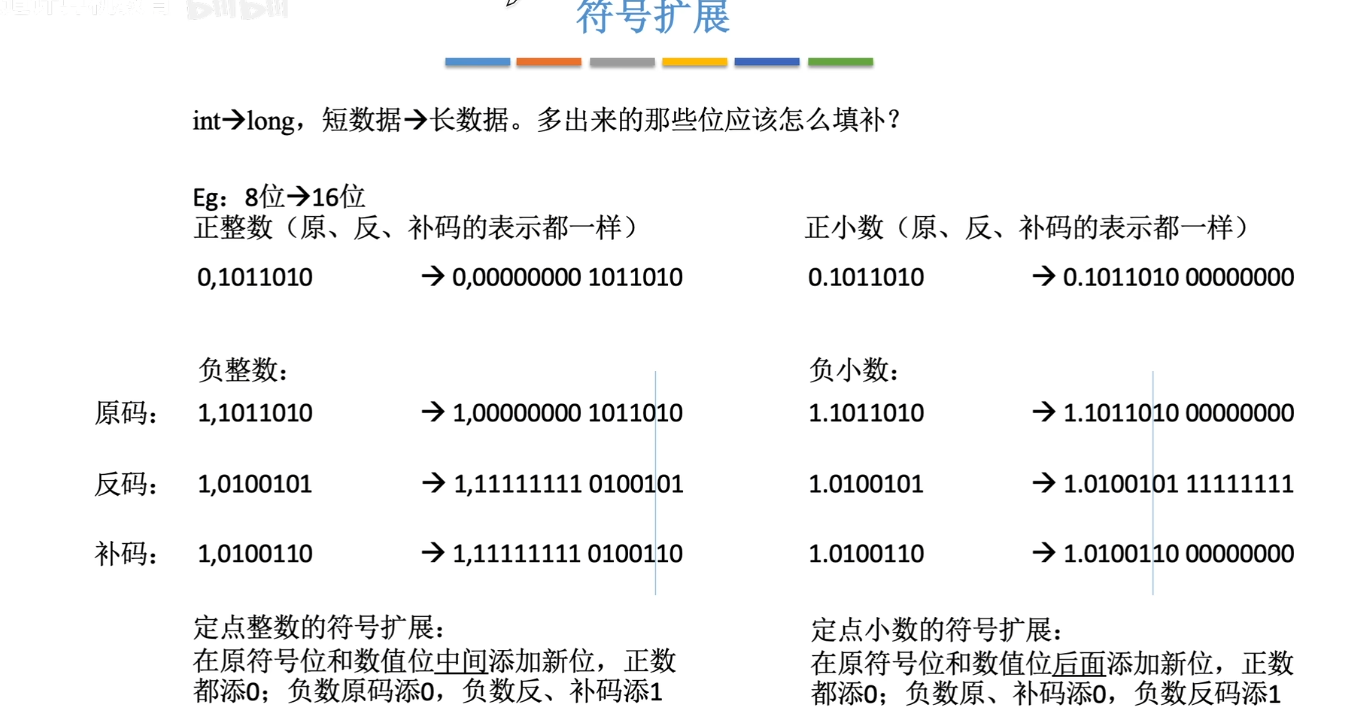
- 定点小数和定点整数在位数扩展时区别
定点小数:x = 1.110 扩展4位 1.1100
定点整数:x = 1100 扩展4位 1.0001
定点整数扩展在符号位后面与数值中间,定点小数扩展在数值位后面。
5-6、奇偶校验
原理:在数据的首部或者尾部,加入一个校验位,使得数据中1的个数为奇数或者偶数。
假设采用奇数校验,则数据中1的个数为奇数,校验位为0。偶校验相反
如 1001101 加入校验位为偶数,则数据中1的个数为4个,为偶数。则数据最终为11001101。
1000101加入校验位为奇数。则数据中1的个数为3个,为奇数。则数据最终为01000101。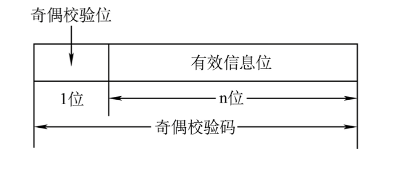
偶数个数据跳变无法检测出来。
硬件实现:通过异或运算实现。去异或每一位数据得到最终的值就是校验位。
6、电路原理
6-1、加法器设计
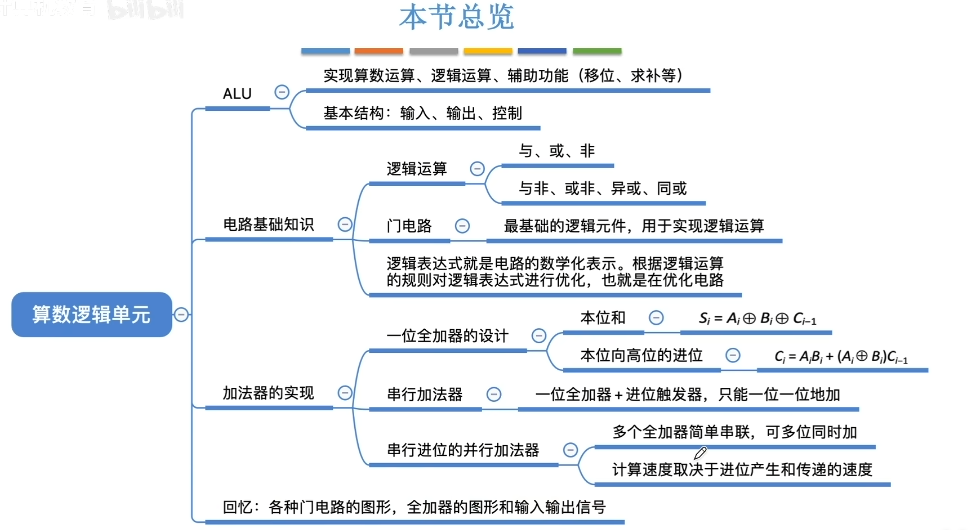
运算器:由MQ,ACC,X,ALU,PSW组成。
算数逻辑单元(ALU): 功能是实现算术运算和逻辑运算。加减乘除,与或非,移位等。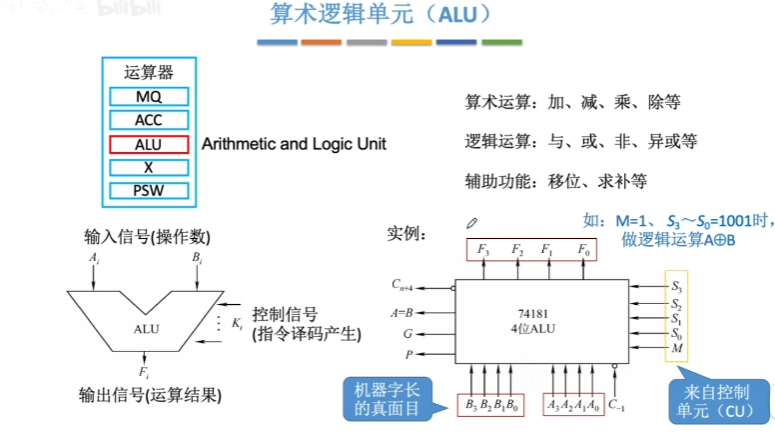
- 逻辑运算
优先级 与 > 或
A(C+D) = AC + AD –分配律
ABC = A(BC) –结合律
A + B + C = A + (B+C) –交换律
反演率–德摩根定律
!(A+B) = !A*!B
!(A*B) = !A+!B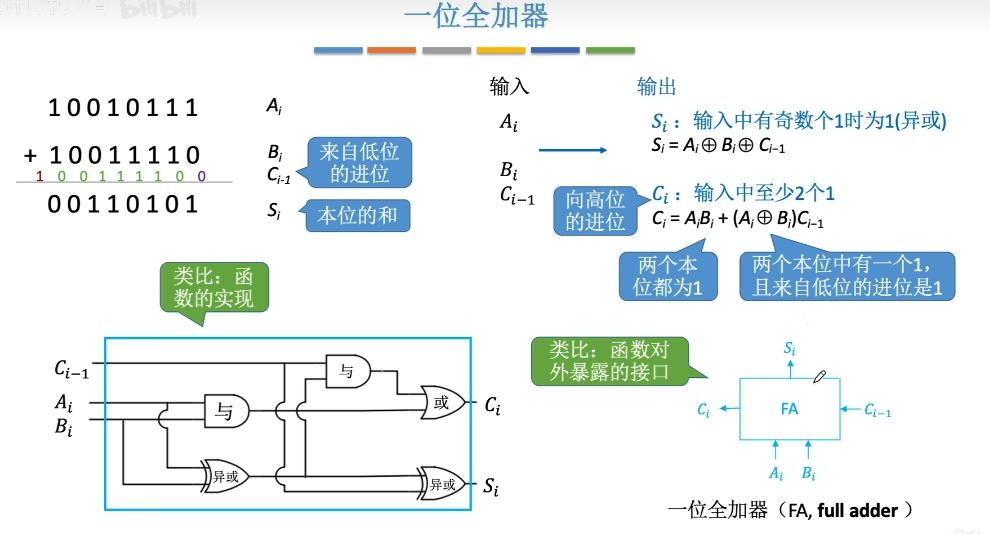
串行加法器
由单个一位全加器串行组成,时间复杂度O(n)并行加法器
由多个一位全加器串行,组成单个n位数,在进行相加,单个n位数相加(也称波形进位)
6-2、并位加法器
这部分心平气和跳过
略
6-3、加法器
无符号数和有符号数都是用同一套电路实现。
区别在于出现溢出时情况不同

6-3-1、加法器溢出
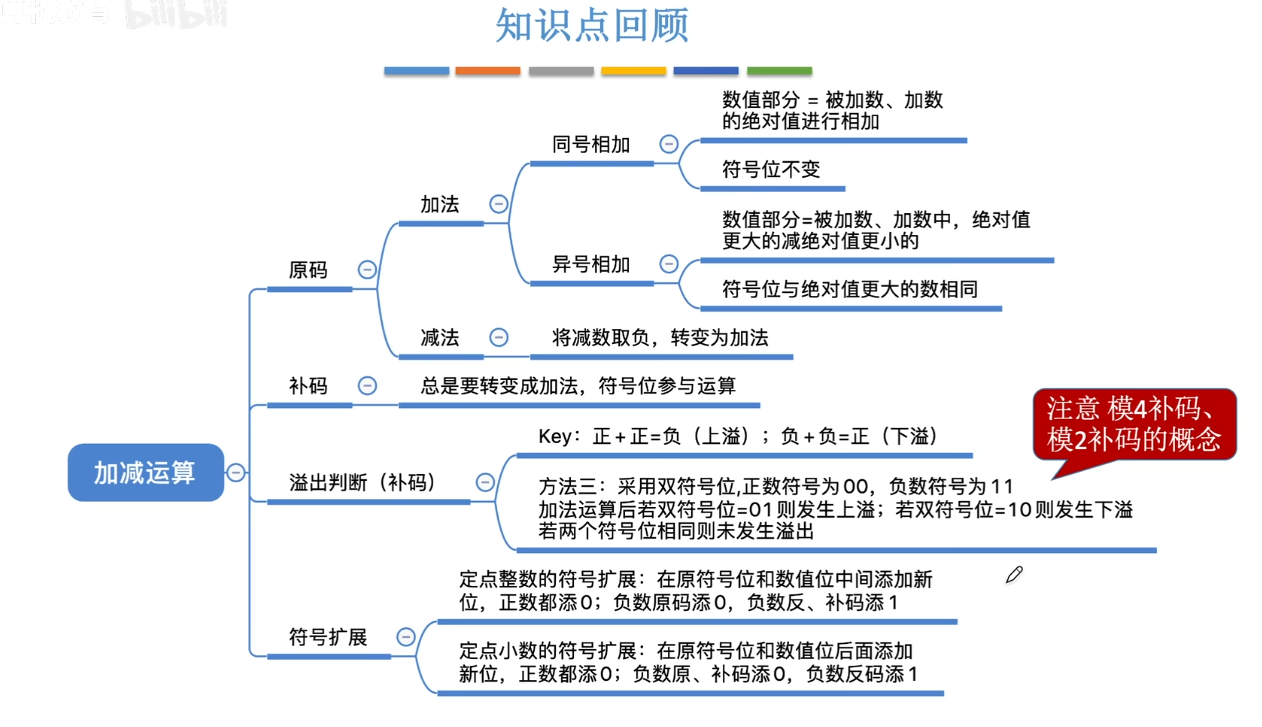
溢出判断:
只有正数和正数相加,才可能出现上溢。
只有负数和负数相加,才可能出现下溢出。
方法一:采用一位符号位

方法二:

- 方法三:
扩展:模的概念:模运算,模m的意义是:如m=4就是,加权值位4包括4后的位舍弃。

- 解决溢出
采用符号扩展的方法
6-4、标志位生成
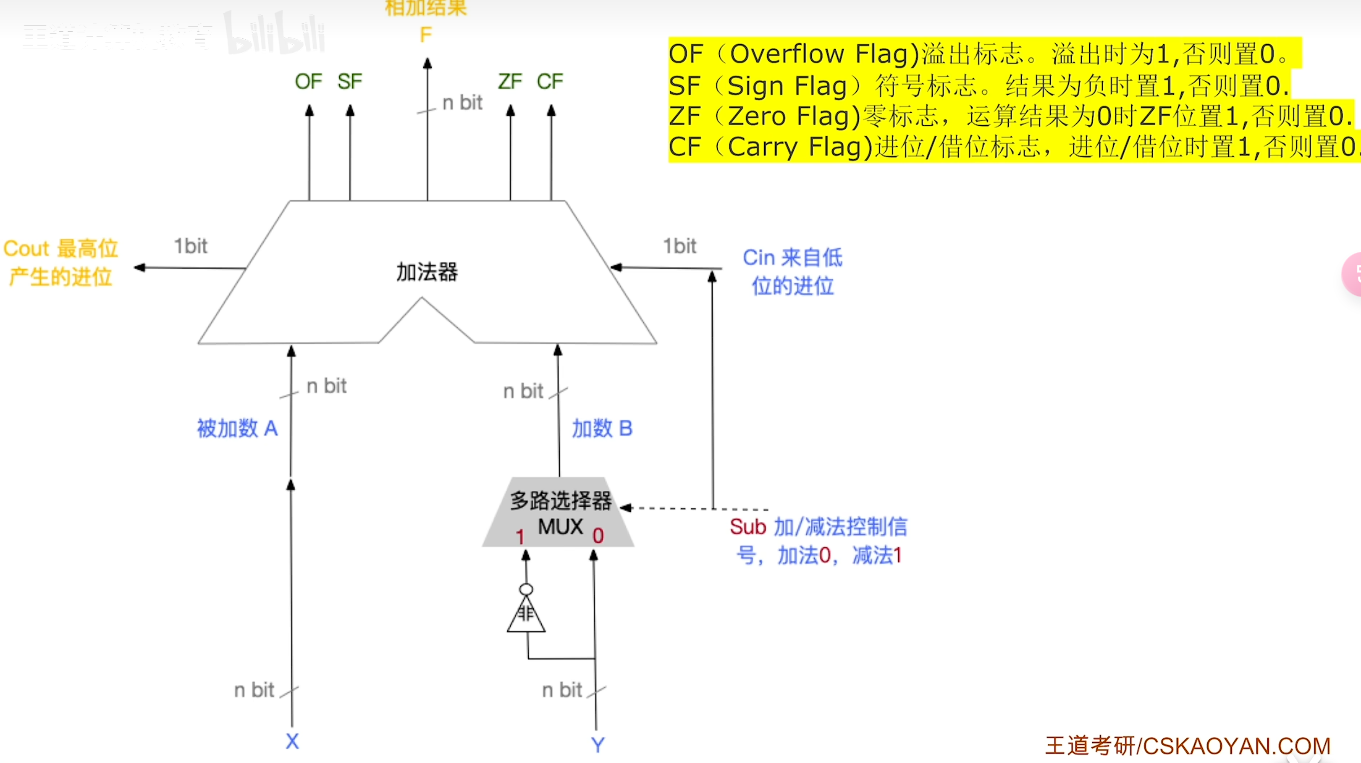
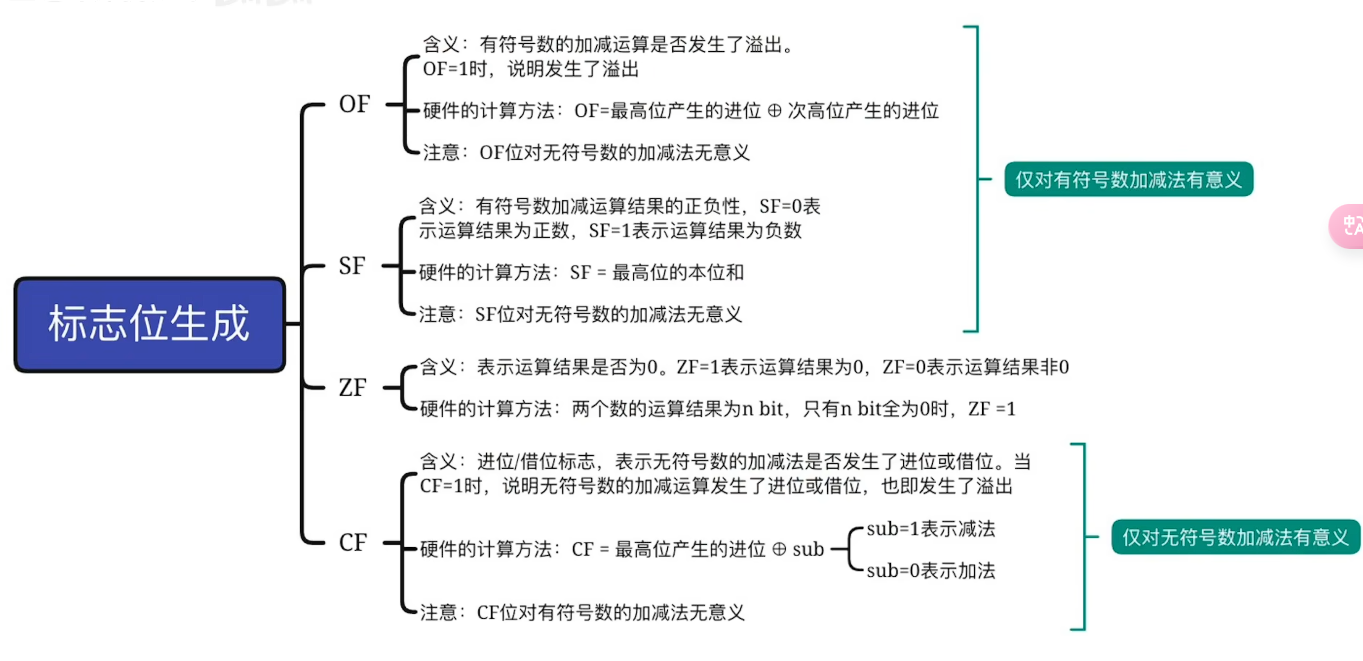
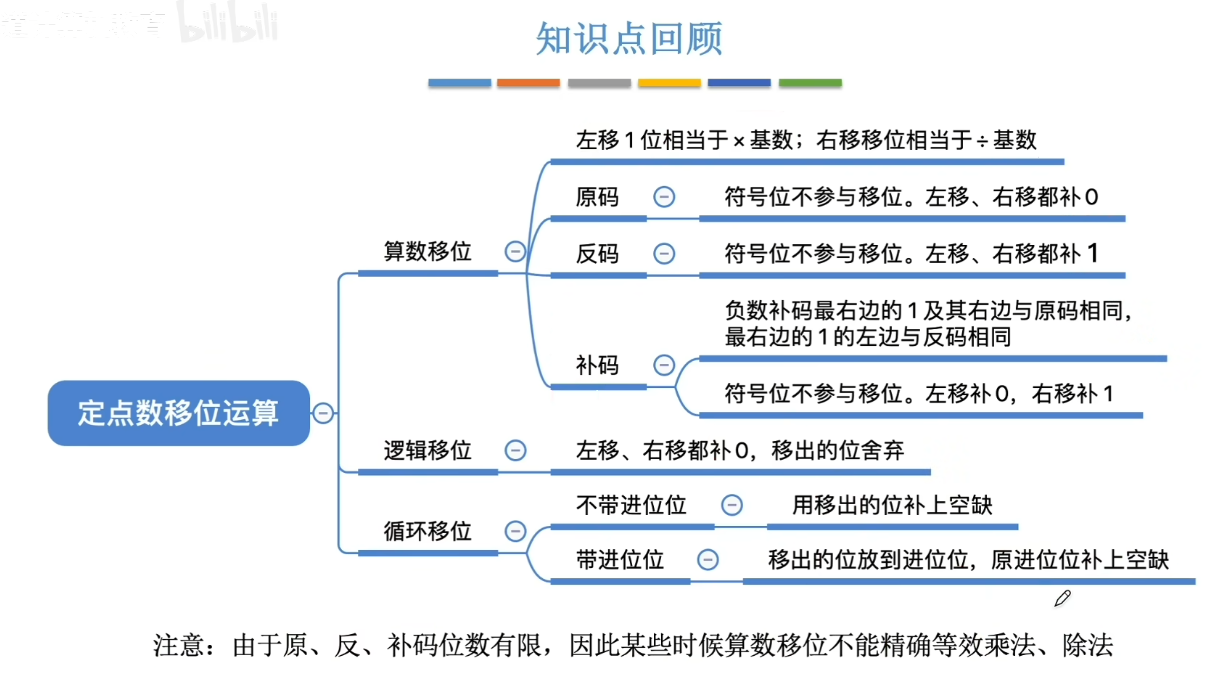
6-5、定点数移位运算
- 算数移位
正数原码算术移位:符号位不变,数值部分左移或右移。溢出的舍弃。如果舍弃的为0,则丢失精度。舍弃的补上0。
正数补码算术移位:和正数原码相同。
正数反码算术移位:和正数原码相同。
负数原码算术移位:符号位不变,数值部分左移或右移。溢出的舍弃。如果舍弃的不为0,则丢失精度。舍弃的补上0。
负数反码算术移位:符号位不变,数值部分左移或右移。溢出的舍弃。如果舍弃的为0,则丢失精度。和原码相反,舍弃的补上1。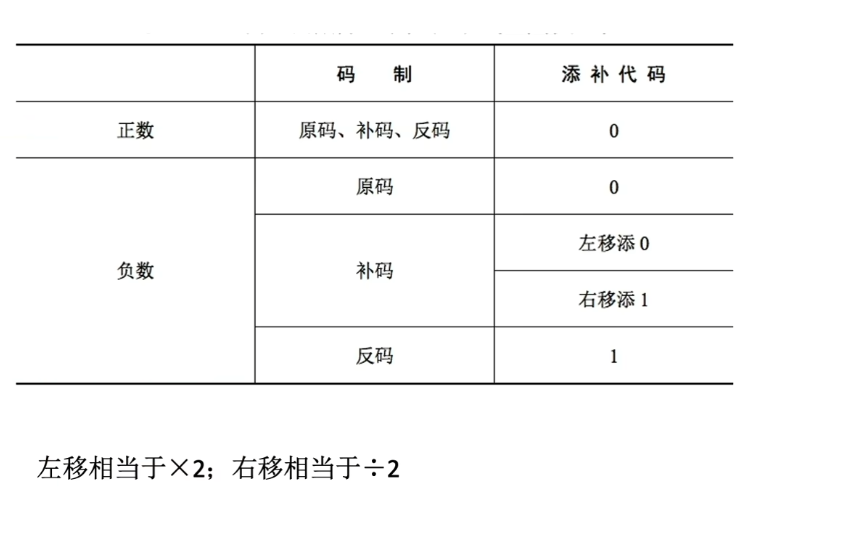
应用:计算机的乘除法运算是利用算数移位实现的。如20*7 = 20 (1+2+22)
- 逻辑移位
逻辑移位:符号位不变,数值部分左移或右移。溢出的舍弃。如果舍弃的为0,则丢失精度。舍弃的补上0。可以把逻辑移位理解为无符号数的算数移位。
应用:一般用于数值拼接。比如把两个8位的数值拼接为16位,左移8位。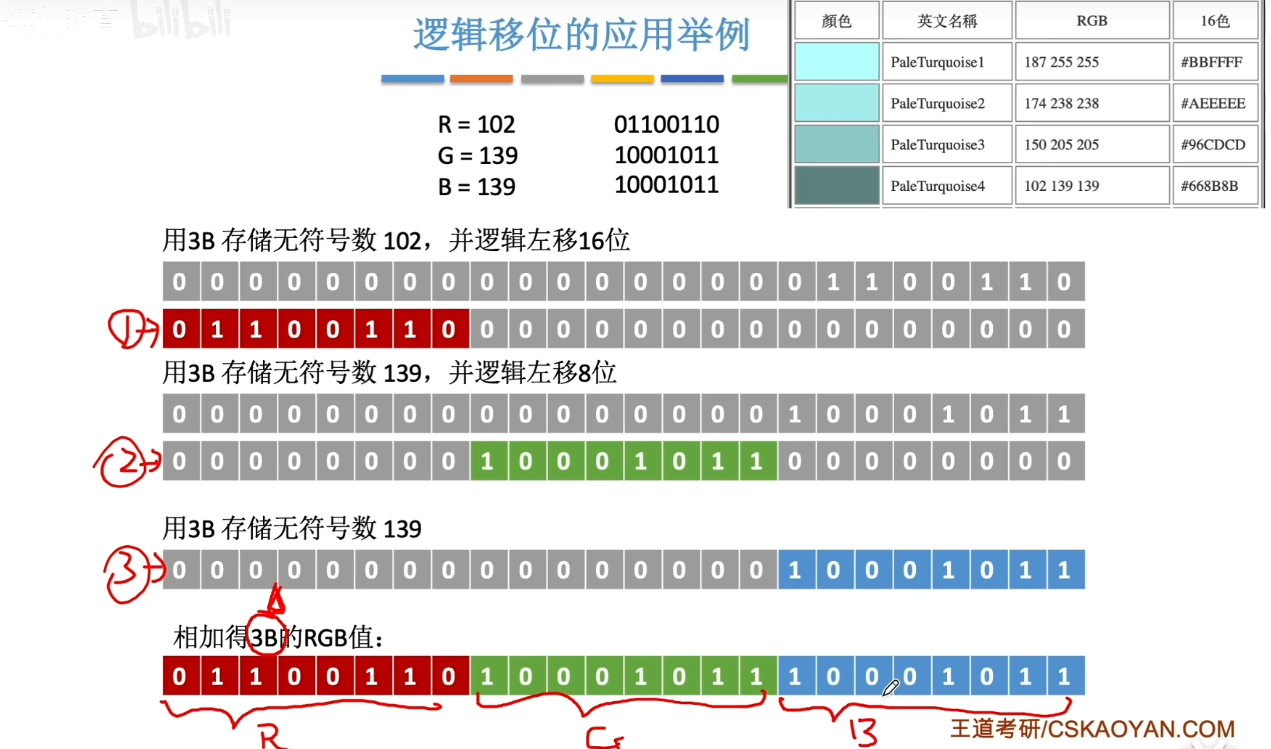
- 循环移位
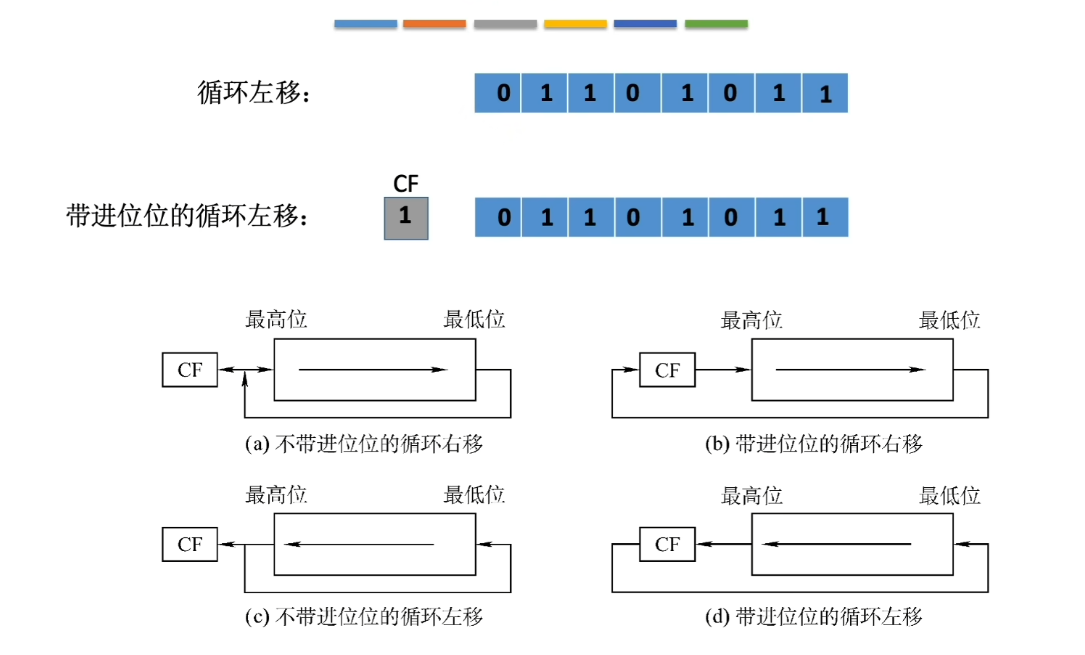
可以用在大小端转换上。大端小端互转。
6-6、定点数的乘法运算
还是r进制思想。如下图:


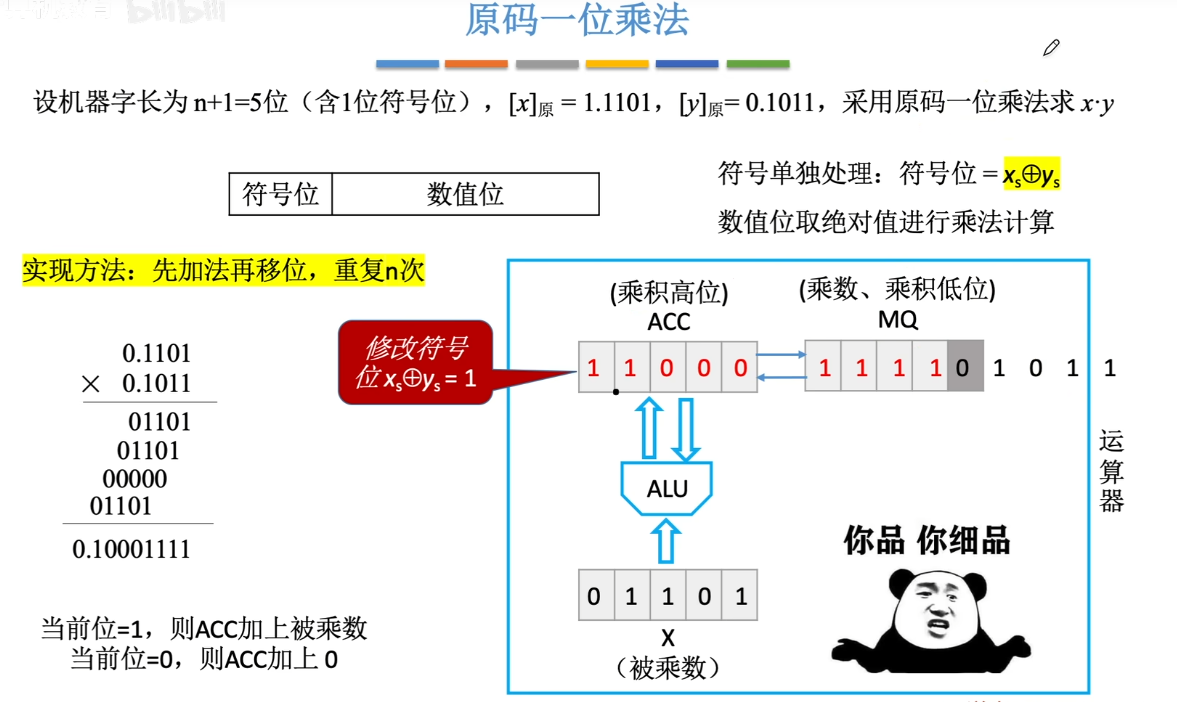
原码的一位乘法:机器字长N+1,数值部分占N位,符号位通过异或确定。数值部分通过被乘数绝对值和乘数绝对值的N轮加法、移位完成,根据当前乘数中参与运算的位确定ACC寄存器加什的数值。若当前位为1,则(ACC)+[|X|]原;R若当前位为0,则(ACC)+0。每一轮ACC、MQ的内容统一逻辑右移。
6-7、补码乘法
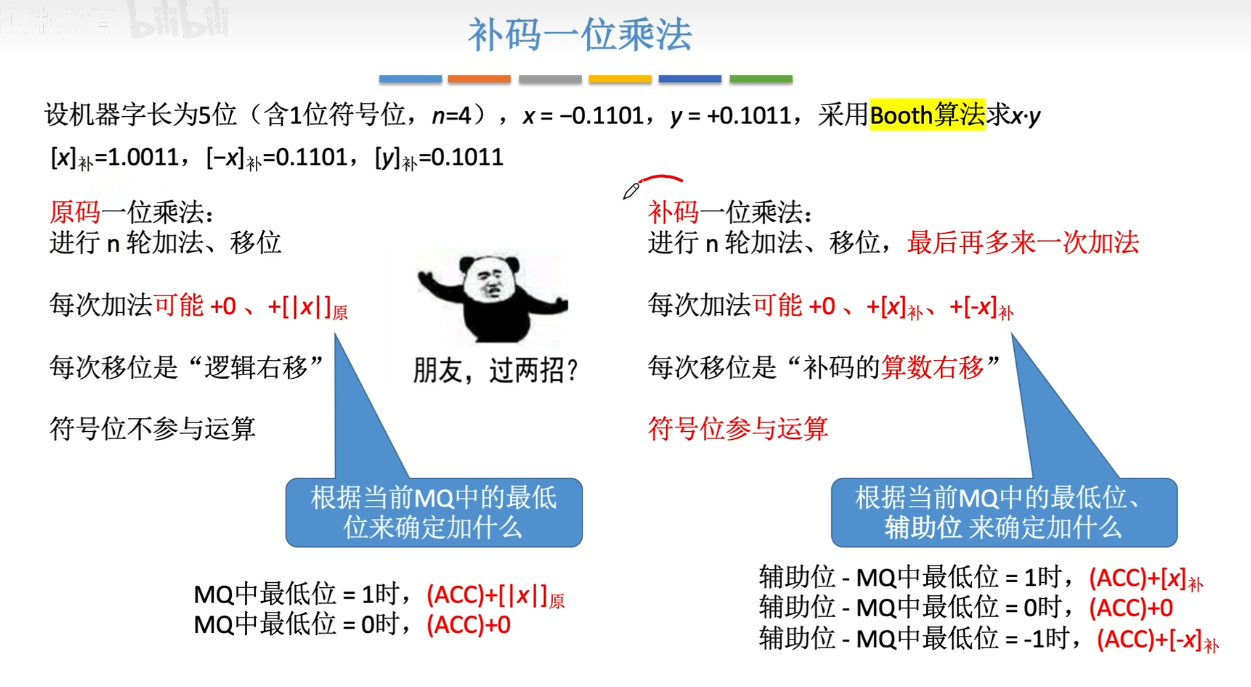
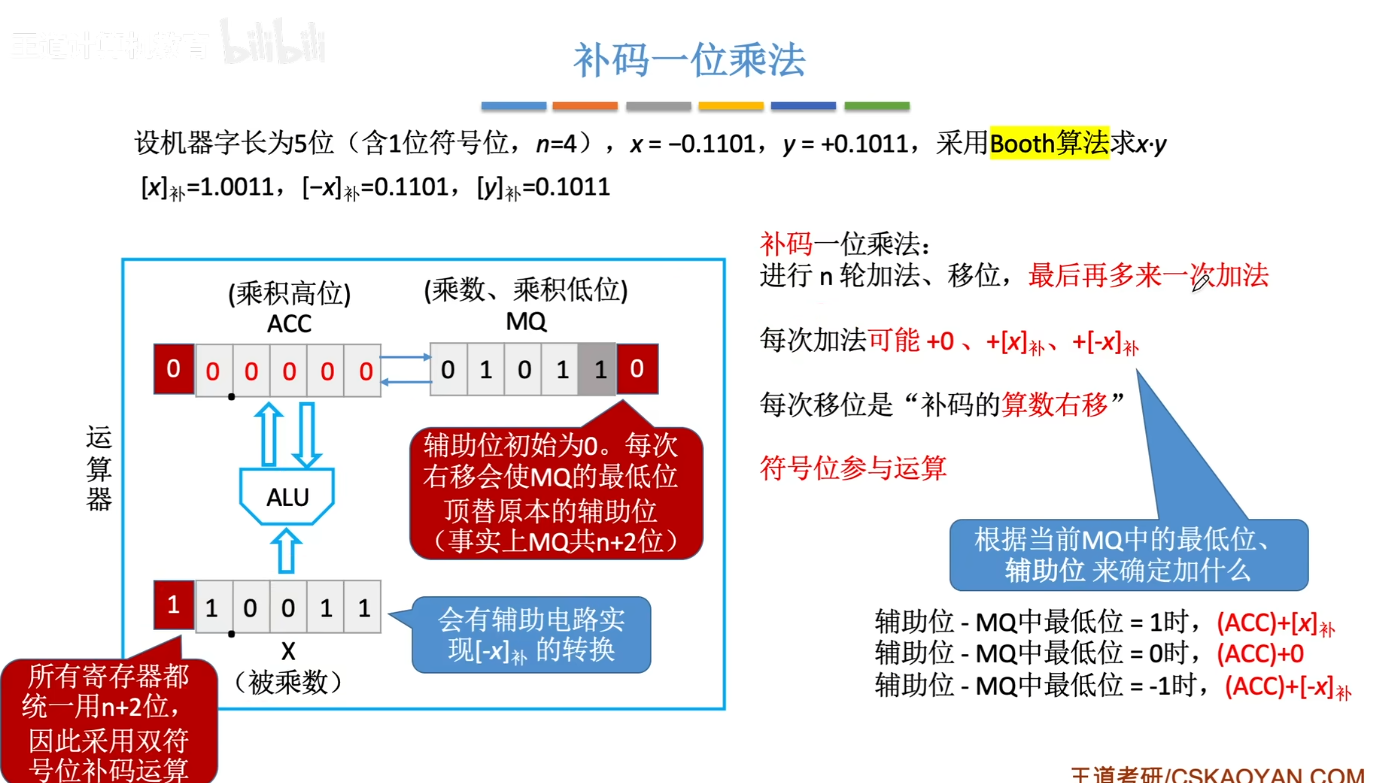

6-8、定点数的除法运算
略–跳过
6-9、补码除法运算
略–跳过
6-10、类型转化

7、数据的存储
大小端模式:大端模式,小端模式。
大端模式:便于人类阅读,小端模式:便于计算机处理。(比如在机器计算时,cpu时从低地址取数据,先读到的就是低字节,便于计算。)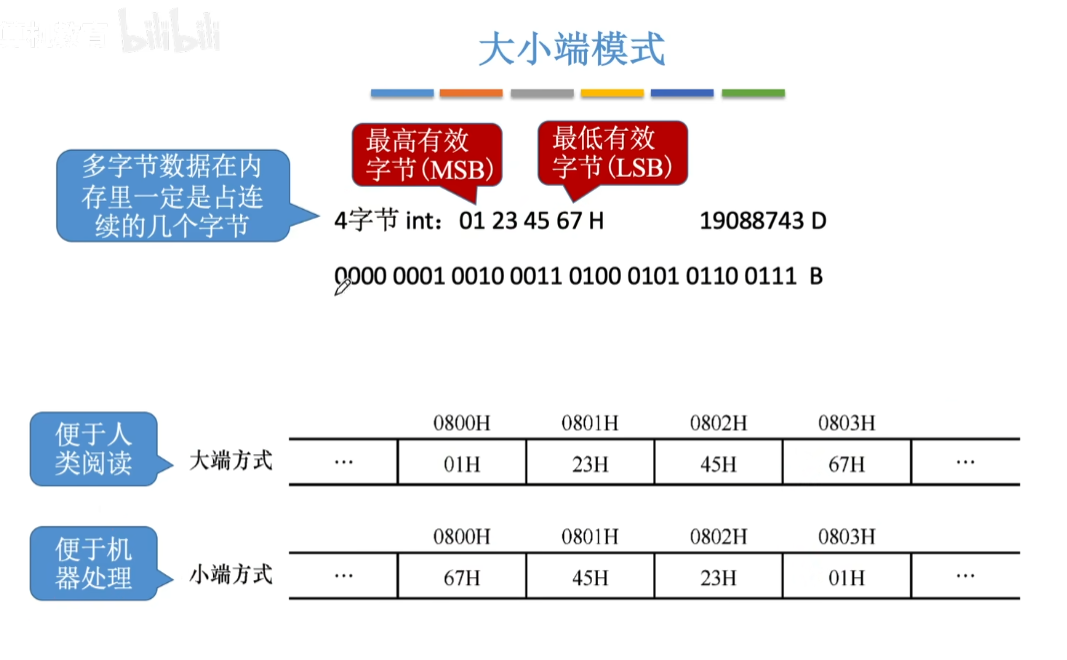
边界对齐问题:为了提高存储效率,通常会将数据按照边界对齐。结构体中常见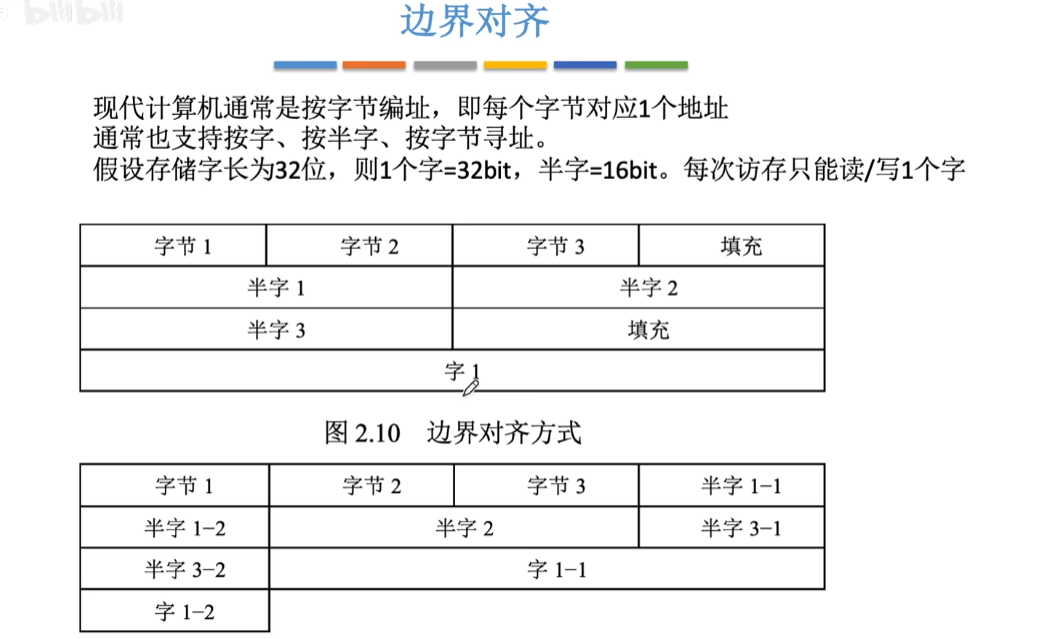
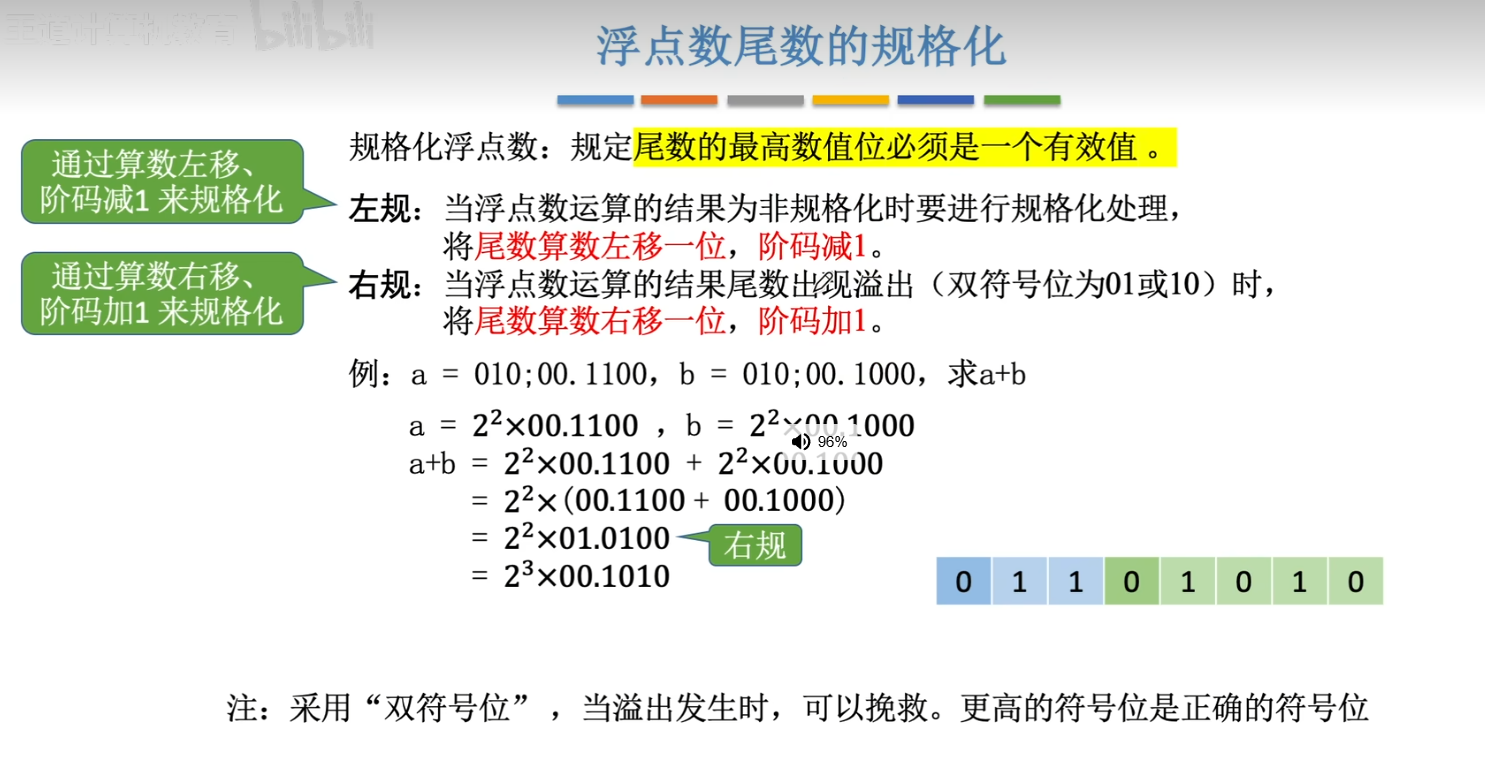
8、浮点数
也就是利用科学计数法的方法

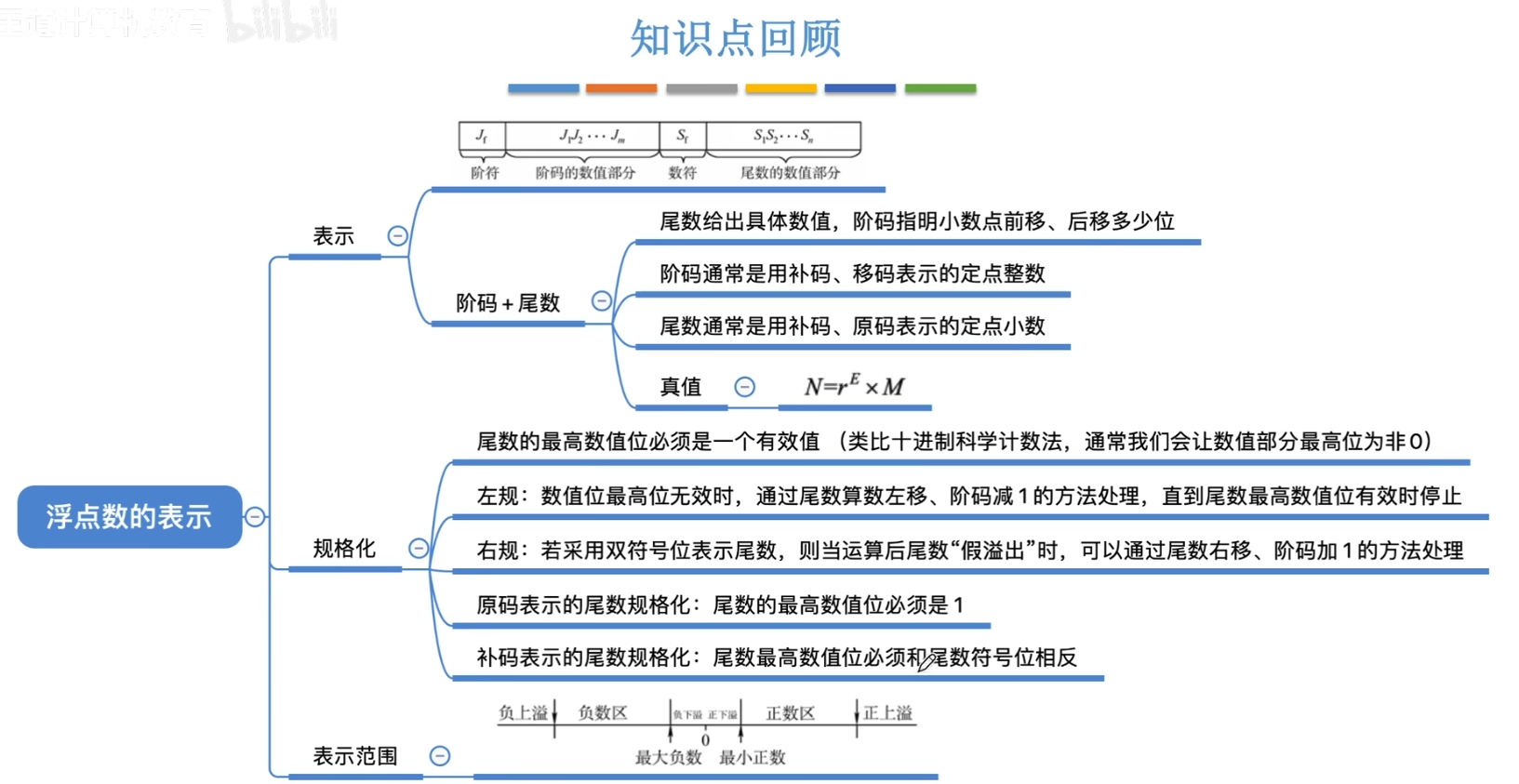
9、IEEE754
规定了浮点数的存储标准
移码:在补码的基础上将符号位取反。只能表示整数。
移码的定义:真值+偏置值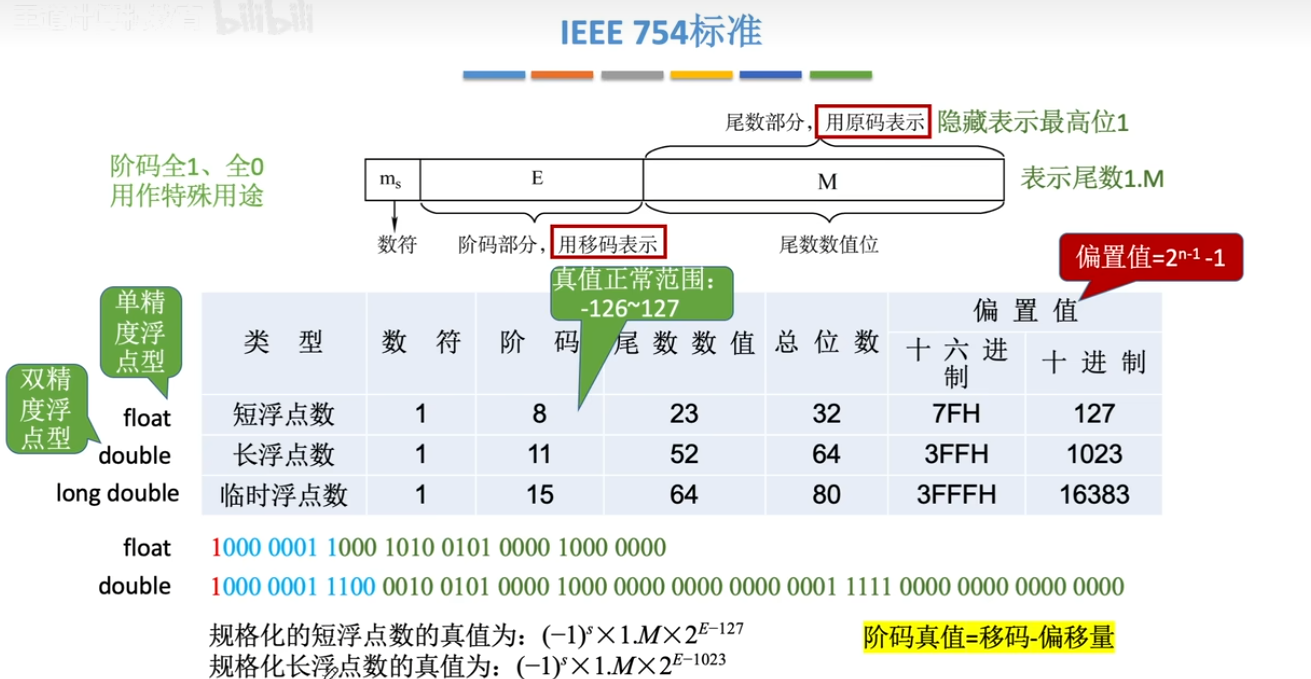
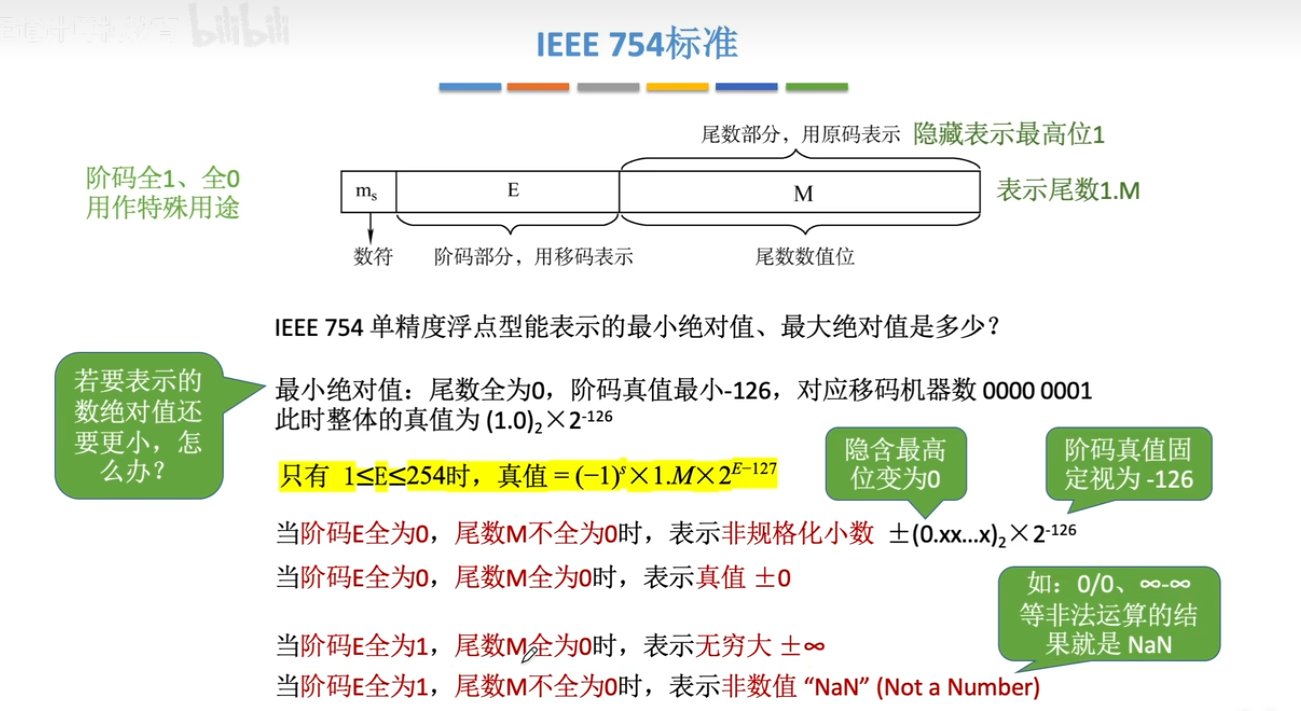
10、浮点数的加减运算
对介,运算,规格化,先跳过
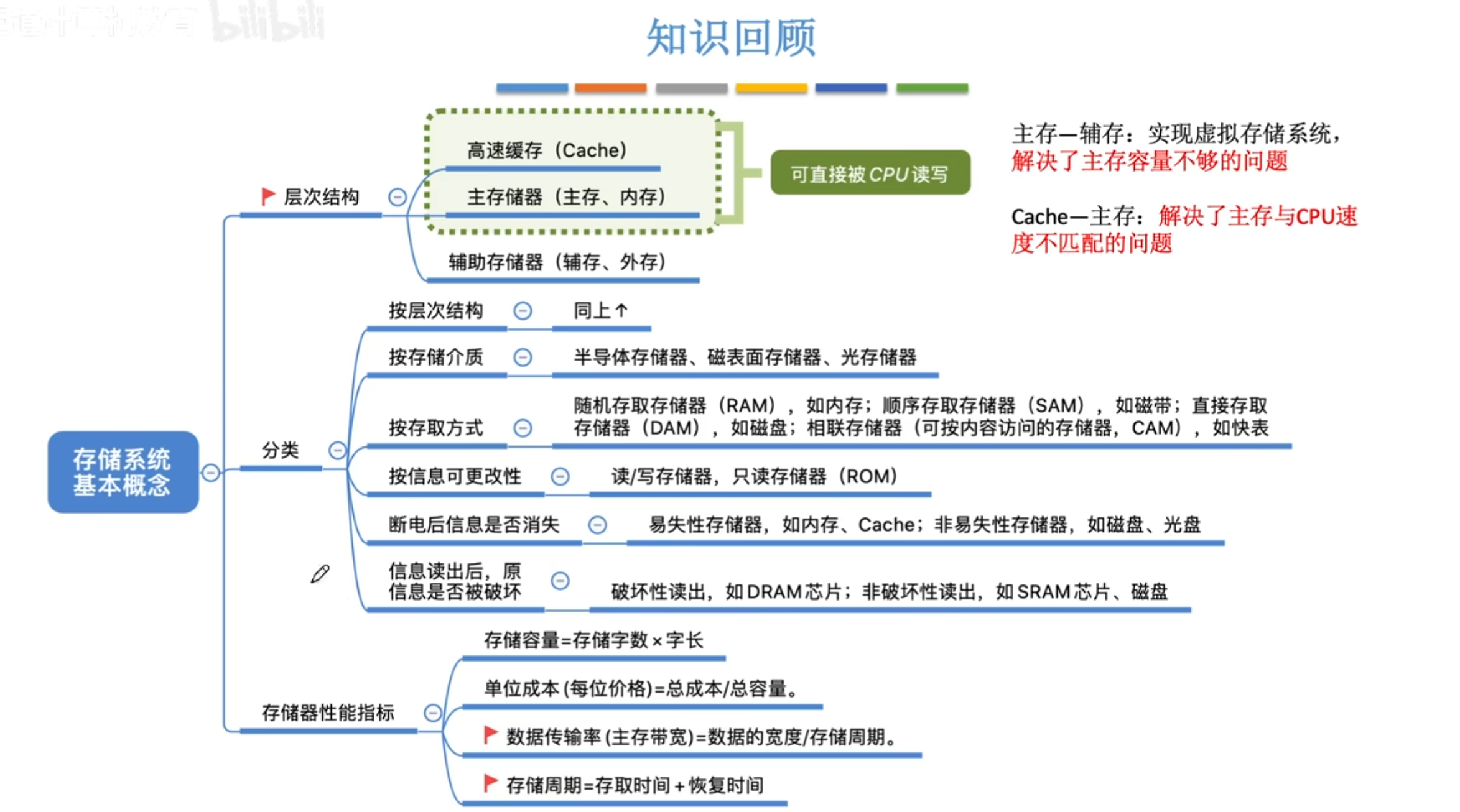
11、存储系统基本概念
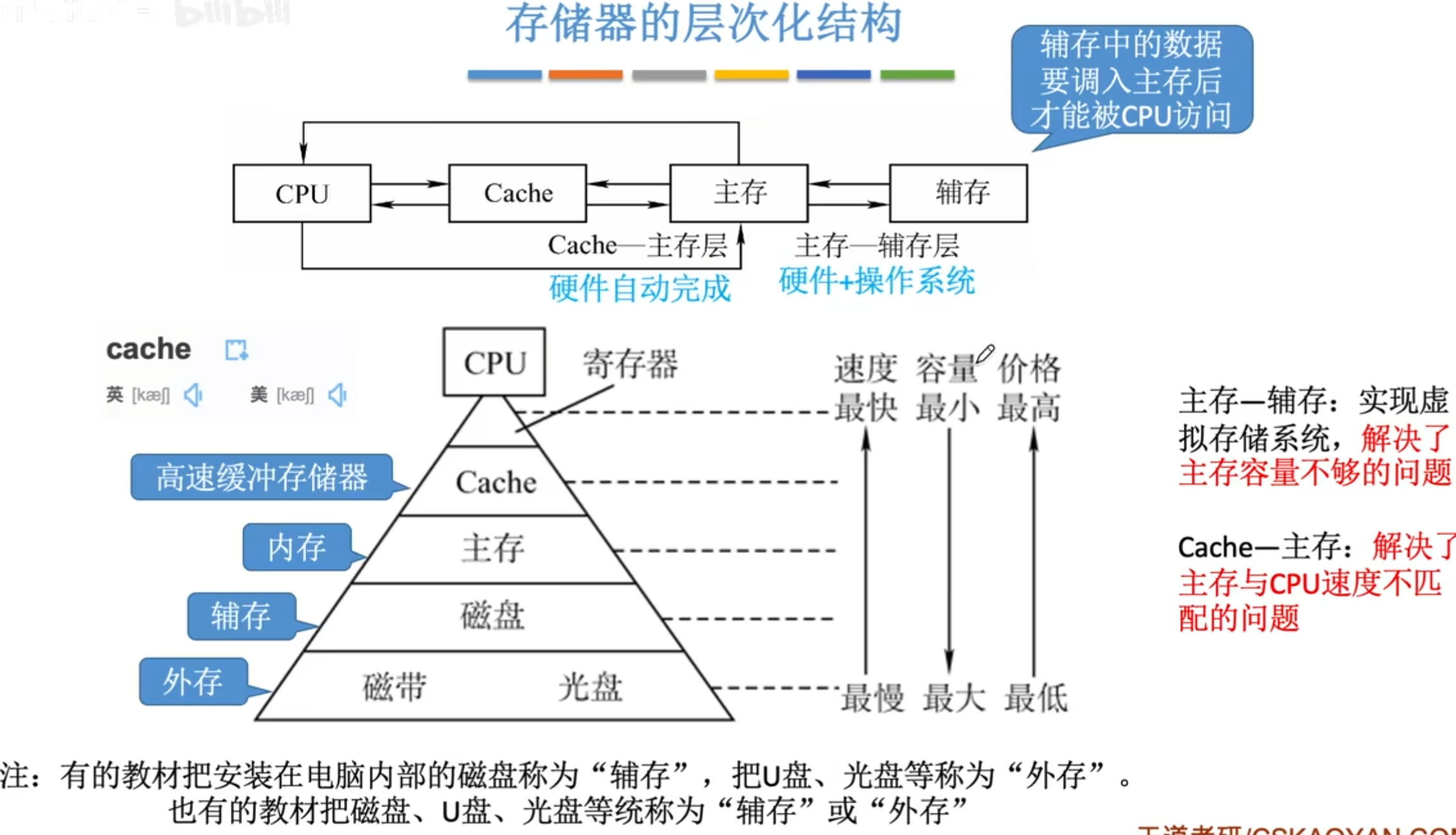
cache层一般软件不用管。由cpu内部缓存。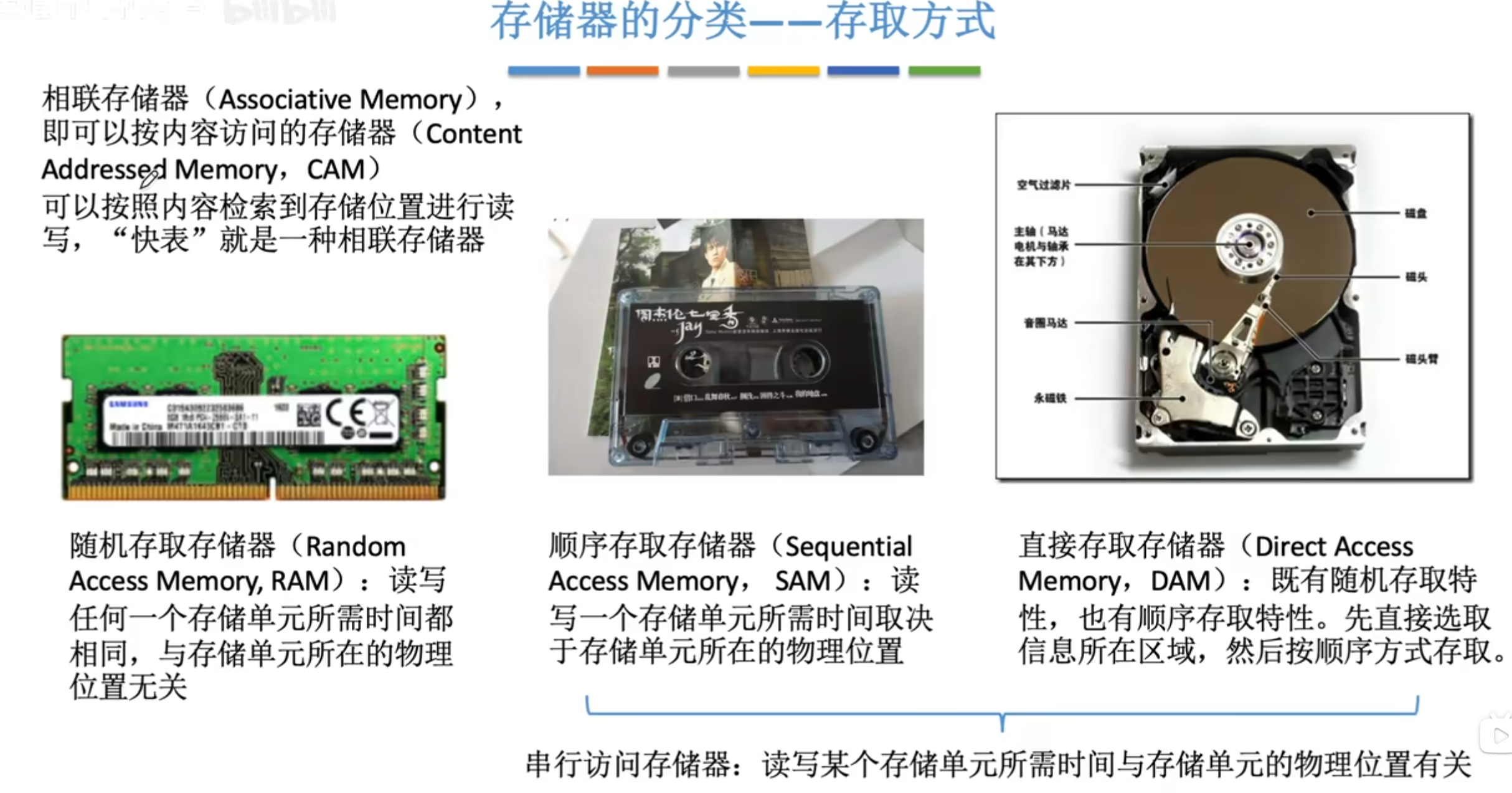
- 按照信息的可更改性,分为可读写和不可读写(只读)。